Solar radiation (Energy)
Solar radiation
| Topics: |
For each second of the solar nuclear fusion process, 700 million tons of hydrogen is converted into the heavier atom helium. Since its formation 4.5 billion years ago, the sun has used up about half of the hydrogen found in its core. The solar nuclear process also creates immense heat that causes atoms to discharge photons. Temperatures at the core are about 15 million degrees Kelvin (15 million degrees C or 27 million degrees F). Each photon that is created travels about one micrometer before being absorbed by an adjacent gas molecule. This absorption then causes the heating of the neighboring atom and it re-emits another photon that again travels a short distance before being absorbed by another atom. This process then repeats itself many times over before the photon can finally be emitted to outer space at the sun’s surface. The last 20% of the journey to the surface the energy is transported more by convection than by radiation. It takes a photon approximately 100,000 years or about 1025 absorptions and re-emissions to make the journey from the core to the sun’s surface. The trip from the sun’s surface to the Earth takes about 8 minutes.
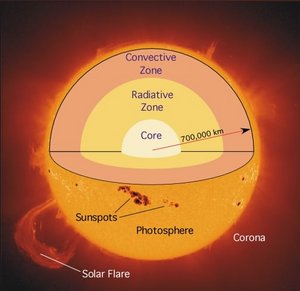
The radiative surface of the sun, or photosphere, has an average temperature of about 5,800 Kelvins. Most of the electromagnetic radiation emitted from the sun's surface lies in the visible band centered at 500 nm (1 nm = 10-9 meters), although the sun also emits significant energy in the ultraviolet and infrared bands, and small amounts of energy in the radio, microwave, X-ray and gamma ray bands. The total quantity of energy emitted from the sun's surface is approximately 63,000,000 Watts per square meter (W/m2 or Wm-2).
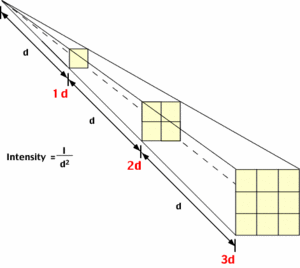
The energy emitted by the sun passes through space until it is intercepted by planets, other celestial objects, or interstellar gas and dust. The intensity of solar radiation striking these objects is determined by a physical law known as the Inverse Square Law (Figure 3). This law merely states that the intensity of the radiation emitted from the sun varies with the squared distance from the source. As a result of this law, if the intensity of radiation at a given distance is one unit, at twice the distance the intensity will become only one-quarter. At three times the distance, the intensity will become only one-ninth of its original intensity at a distance of one unit, and so on.
Given the amount of energy radiated by the sun and the average Earth-sun distance of 149.5 million kilometers, the amount of radiation intercepted by the outer limits of the atmosphere (Atmosphere layers) can be calculated to be around 1,367 W/m2. Only about 40% of the solar energy intercepted at the top of Earth's atmosphere passes through to the surface. The atmosphere reflects and scatters some of the received visible radiation. Gamma rays, X-rays, and ultraviolet radiation less than 200 nanometers in wavelength are selectively absorbed in the atmosphere by oxygen and nitrogen and turned into heat energy. Most of the solar ultraviolet radiation with a range of wavelengths from 200 to 300 nm is absorbed by the concentration of ozone (O3) gas found in the stratosphere. Infrared solar radiation with wavelengths greater than 700 nm is partially absorbed by carbon dioxide, ozone, and water present in the atmosphere in liquid and vapour forms. Roughly 30% of the sun's visible radiation (wavelengths from 400 nm to 700 nm) is reflected back to space by the atmosphere or the Earth's surface. The reflectivity of the Earth or any body is referred to as its albedo, defined as the ratio of light reflected to the light received from a source, expressed as a number between zero (total absorption) and one (total reflectance).
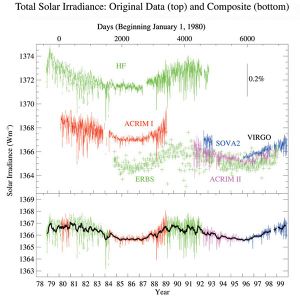
For general purposes, the energy output of the sun can be considered constant. This of course is not entirely true. Scientists have shown that the output of the sun is temporally variable (Figure 4). Some researchers have also suggested that the increase in the average global temperature over the last century may have been solar in origin. This statement, however, is difficult to prove because accurate data on solar output of radiation only goes back to about 1978.
Further Reading
