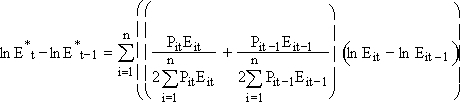Net energy analysis
Contents
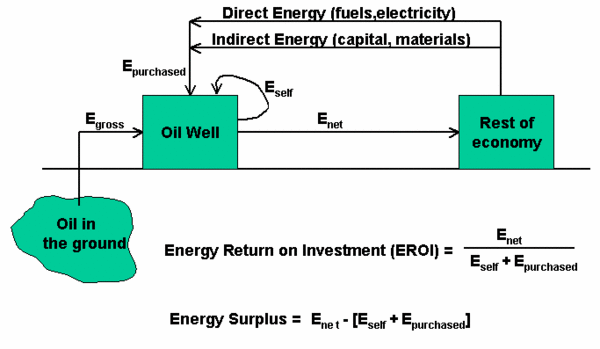
- 1 Introduction One technique for evaluating energy systems is net energy analysis, which seeks to compare the amount of energy (Net energy analysis) delivered to society by a technology to the total energy required to find, extract, process, deliver, and otherwise upgrade that energy to a socially useful form. Energy return on investment (EROI) is the ratio of energy delivered to energy costs (see Figure 1). Biophysical and ecological economists argue that net energy analysis has several advantages over standard economic analysis. First, net energy analysis assesses the change in the physical scarcity of energy resources, and therefore is immune to the effects of market imperfections that distort monetary data. Second, because goods and services are produced from the conversion of energy into useful work, net energy is a measure of the potential to do useful work in economic systems. Third, EROI can be used to rank alternative energy supply technologies according to their potential abilities to do useful work in the economy. Most neoclassical economists reject methods of economic analysis that are not based on human preferences, arguing that net energy analysis does not generate useful information beyond that produced in a thorough economic analysis.
- 2 Energy Versus Economic Analysis
- 3 Methods of Net Energy Analysis
- 4 Energy Aggregation and Energy Quality
Introduction One technique for evaluating energy systems is net energy analysis, which seeks to compare the amount of energy (Net energy analysis) delivered to society by a technology to the total energy required to find, extract, process, deliver, and otherwise upgrade that energy to a socially useful form. Energy return on investment (EROI) is the ratio of energy delivered to energy costs (see Figure 1). Biophysical and ecological economists argue that net energy analysis has several advantages over standard economic analysis. First, net energy analysis assesses the change in the physical scarcity of energy resources, and therefore is immune to the effects of market imperfections that distort monetary data. Second, because goods and services are produced from the conversion of energy into useful work, net energy is a measure of the potential to do useful work in economic systems. Third, EROI can be used to rank alternative energy supply technologies according to their potential abilities to do useful work in the economy. Most neoclassical economists reject methods of economic analysis that are not based on human preferences, arguing that net energy analysis does not generate useful information beyond that produced in a thorough economic analysis.
Energy Versus Economic Analysis
The energy events of the 1970’s raised the issue of whether economic measures such as price or cost accurately captured all the relevant features of an energy supply process. Economists generally argue that, by definition, the price of a fuel automatically captures all such relevant features. Yet, a strong case can be made that the standard economic approach to measuring the economic usefulness of a fuel yields one type of information and only partially informs us about all relevant aspects of resource quality. Net energy analysis, through the calculation of EROI, informs us about some of those other qualities, such as the potential for a fuel source to yield useful energy to the rest of the economy. Such qualities may or may not be reflected in a fuel’s price. As Peet et al, 1987, stated:
...we believe the conventional economic perception of the ‘value’ of primary energy resources is incomplete and potentially misleading, in that it does not adequately take account of the factors which constrain a society’s ability to obtain useful consumer energy from such sources.
In part because it rejects economic measures of value as necessary and sufficient expressions of resource quality, net energy analysis has been a very controversial analytical tool, generating vigorous and sometimes acrimonious exchanges between net energy analysis practitioners and economists. The debate between net energy analysts and economists became a very heated one for several reasons. One reason is that many economists viewed net energy analysis as another physical model of scarcity which, like the classical economic scarcity model and The Limits to Growth physical models, is obviously inferior to the neoclassical view of scarcity. Many grandiose and unsubstantiated claims were made about the immunity net energy analysis enjoyed from many of the problems facing economic analysis, making it a superior decision-making tool. Some energy analysts, such as Odum, Hannon, and Costanza, proposed a theory of economic and social value based on energy, which economists were quick to criticize.
Economists naturally, and quite justifiably in some cases, reacted very strongly to some of the extreme claims made by some energy analysts. Economists questioned the assumptions and methods of net energy calculations as well as the usefulness of net energy results for energy and economic policy. At the same time, many critics rejected net energy analysis in its entirety based on the reasonableness of claims made by some energy analysts which were not shared by energy analysts in general. In the process, the nuts and bolts of net energy analysis and it’s usefulness in assessing resource quality escaped the objective discussion it deserved. A review of this literature also indicates that some economists engaged in the net energy debate lacked sufficient knowledge of basic ecological and thermodynamic principles to accurately judge the assumptions and methods of net energy analysis, much less its conclusions. Due to this lack of knowledge and to the perceived threat of net energy analysis as a purported replacement for economic analysis, some economists criticized and rejected net energy analysis on the basis of claims never made by its practitioners.
Energy Analysis and Policymaking
Given 25 years of hindsight, it is useful to review the net energy analysis debate. Much of this debate is a matter of public record, some of which is reviewed in Hall et al, 1986.
Net energy analysts promote their discipline using a range of arguments. Gilliland argued that compared with economic analysis, net energy analysis of alternative energy technologies can provide more information of a less conflicting nature to policy makers. Similarly, the Government Accounting Office (GAO) argued that the strength of net energy analysis is that it gives policy makers the opportunity to consider the EROI of an energy technology independent of its profit potential and other financial considerations. Participants at a conference devoted to the critique of net energy analysis concluded that it was a useful tool where market imperfections distorted dollar values. It was also argued that net energy analysis was useful for technology evaluation, particularly in the identification of potential areas for energy conservation. Bullard made an analogy between net energy analysis and environmental impact statements, arguing that quantitative assessments of the impact of new technologies may provide information to policy makers in the same way the environmental impact statements address external effects not adequately dealt with in the market. Chapman et al. cited three reasons why net energy analysis of energy technologies is desirable. First, the energy processing sectors of most industrial nations use significant portions of total national energy use and therefore offer a significant potential for energy conservation. Second, waste heat production from fossil fuel conversion poses a major hazard to local and global climate. Third, it is essential to know the energy costs of energy itself in order to assess the energy costs of other goods and services.
Net energy analysis proponents argue that one advantage it holds over economic analysis is that it is not plagued by many of the problems facing monetary analyses. Energy analysts have argued that inflation, subsidies, regulations, uncertainty about future prices and discount rates, and other market imperfections prevent monetary analyses from making consistently accurate assessments of energy technologies. Others are concerned that subsidies to some energy technologies can prevent the market from detecting whether a fuel is at or near the energy break-even point. Herendeen argued that net energy analysis is particularly important for highly touted technologies such as gasohol and the solar power satellite which are subsidized with tax dollars and do appear to be near the energy break-even point.
Other energy analysts have argued because it is based on dollar profitability, economic cost-benefit analysis cannot accurately measure the direct and indirect energy inputs to a process, something net energy analysis was designed to do. A detailed understanding of the direct and indirect energy costs of energy production is critical to Federal decisions on funding competing energy technologies. Energy analysts argue that this quality gives their models a significant advantage over economic analysis in the effort to evaluate future energy supply and demand. As Slesser, 1977, stated:
Because of a better handle on the future energy requirements for production, as opposed to discounted money costs of production, energy analysis gives a faster signal of impending change. Where energy analysis can be of immense value is in normative forecasting, hence its value to technology assessment and demand forecasting.
Many economists have rejected these claims made by energy analysts. For example, critics have rejected Gilliland’s sweeping claim that the results of net energy analysis do not change when dollar values change due to inflation or changes in the discount rate. Critics argue that net energy results are sensitive to market circumstances, and therefore subject to change over time just like monetary analyses. Thus, net energy analysis may not be a better allocator of resources where market imperfections exist. Critics point out that EROI calculations are market-determined to the degree that they depend on the technology, industry structure, discount rate, and prices that exist at the time. Changes in any of those factors will undoubtedly alter the energy costs of goods, and thereby alter the results of net energy analysis. As Huettner, 1976, argues:
A net energy analysis of a specific technology, such as the present nuclear fuel cycle and its supporting techniques, depends on the prices, discount rates, and other market conditions existing at the time it was made. As prices change through time, the energy content of steel, copper, cement, and all other inputs used in the nuclear fuel cycle are likely to change because of substitution effects, even if there is no change in technology and market structure.
Net Energy Analysis as a Normative Technique
Many critics of net energy analysis have erroneously assumed that all practitioners believe in an energy theory of value. Some energy analysts have proposed an energy theory of value, where the value of goods and services are assumed to related to the direct and indirect energy embodied in them. Costanza has offered empirical evidence for an embodied energy theory of value. It is safe to say, however, that the vast majority of net energy analysts reject an energy theory of value while embracing the usefulness of net energy calculations, and also argue that the usefulness of net energy analysis does not hinge on whether or not an energy theory of value is "valid". Most energy analysts view net energy analysis as a complement to the results of standard economic analysis, which is always subject to varying degrees of uncertainty and error.
Nevertheless, some critics argue that net energy analysis should be judged by whether or not its conclusions have normative implications. Having constructed their own straw man, such critics reject net energy analysis because it is a mechanistic tool void of any real value content. Hyman, for example, states that net energy has no connection to social welfare, therefore net energy analysis is not a useful policy tool since it doesn’t help satisfy human wants. Similarly, Webb and Pearce argue that net energy analysis cannot be used, for example, to rank alternative energy technologies because such a procedure requires the specification of an objective function, a normative issue net energy analysis is not equipped to deal with, unless an energy theory of value is assumed. The usefulness of net energy analysis does not depend on its normative value in the sense implied by the aforementioned critics. Resolution of questions such as whether society is maximizing a net energy objective function or whether an energy theory of value is valid is irrelevant to the issue of whether net energy analysis is useful in the overall assessment of resource quality. A more relevant test is whether net energy analysis yields any unique and useful information about the economic usefulness of a fuel which cannot be obtained from other types of analysis. The fact that society is not maximizing a net energy function is not legitimate grounds for dismissing net energy analysis as a useful input to an overall decision-making process.
There are no right or wrong answers to these issues, making it impossible to state just how "physical" a measure the EROI is, or how "economic" prices are. The important point is that any analysis which posits to bridge the two approaches should explicitly recognize and consider their different assumptions and value judgements. EROI emphasizes the physical underpinnings of scarcity, while acknowledging the importance of economic factors. It implicitly assumes that changes in the energy cost of energy have important economic implications that may or may not be reflected in prices.
The economic significance of the EROI does not hinge on the existence or nonexistence of a causal link between changes in the EROI and changes in the structure and direction of change in the economy. Such a relationship or any other form of "energetic determinism" has been neither demonstrated nor argued for here. Social and cultural factors merit equal consideration. For example, both Cottrell and Cook described how many societies rejected the opportunity to adopt a higher EROI fuel source because such a transition threatened existing social patterns to the degree that sufficient opposition prevented that transition. Human factors, however, have dominated the development of our perspective of the relationship between nature and society since at least the Industrial Revolution, and in particular have influenced how we describe and measure the economic impacts of changes in resource quality. A balanced view of these issues requires an understanding of the physical framework in which all human ideas, institutions, and aspirations must operate.
Methods of Net Energy Analysis
Net energy analysis seeks to assess the direct and indirect energy required to produce a unit of energy. Direct energy is the fuel or electricity used directly in the extraction or generation of a unit of energy. An example is the natural gas burned in engines that pump oil to the surface. Indirect energy is the energy used elsewhere in the economy to produce the goods and services used to extract or generate energy. An example is the energy used to manufacture the drilling rig used to find oil. The direct and indirect energy use is called embodied energy. Both the energy product and the embodied energy can be expressed in common physical units of measurement, such as Btus.
The Energy Cost of the Factors of Production
To calculate the energy cost of energy, or for that matter any good or service, we must be able to quantify in energy terms the fuel, capital, materials, and labor used in the extraction and processing of the energy in question. The energy equivalents of the factors of production can be calculated in one of several rather straightforward methods to be discussed shortly, using readily available data on annual flows of fuels and other materials through the economy.
Fuel
The energy costs associated with a fuel have two components: the quantity of energy released on combustion (enthalpy) and the energy required to extract, process, and deliver it to the customer. The first component is called the chemical energy of the fuel and usually is measured by the heat given off by combusting the fuel. For example, a 42-gallon barrel of refined crude oil releases approximately 1.5 million kilocalories of heat when combusted.
The second component of energy consists of processing energy, the energy used by an energy transformation process to secure additional energy supplies. The sum of all such processing energies is the embodied energy cost of a fuel. The embodied energy in a barrel of oil includes the energies required to produce and operate drilling rigs, pipelines, and refineries, as well as the energies used to house and support the geophysicists and other individuals who work in the oil business.
It is important to note that a fuel’s embodied energy is not a thermodynamic property of that fuel. Rather, it is an accounting procedure that measures the direct plus indirect energy content of fuel. When a fuel is combusted only the potential energy stored in its chemical bonds is able to do economic work. Nevertheless both the embodied energy of a fuel and its heat from combustion are energy costs of commodities whose production requires the combustion of fuel.
Capital
Capital can be viewed as economic energy invested in machines and tools that replace or empower human labor, thereby making workers more productive and, ultimately, allowing for higher wages. Capital can be used to do economic work that is difficult and/or dangerous for human labor to do alone. Capital also can be used to reduce the quantity of time, fuel, or labor used to produce a good or to provide a service. The energy equivalent of a unit of capital equipment normally is calculated as the quantity of fuel energy used to produce and maintain it. Alternatively, the energy cost of capital can be thought of as the fuel energy or labor energy saved by capital equipment at the margin.
The energy required to produce a dollar’s worth of capital equipment for a given industry is calculated by summing all the fuel used to produce each year’s new capital according to the appropriate standard industrial classifications. For example, in 1979, Standard Industrial Classification (SIC) sector 3553 (Woodworking Machinery) used 3.1 trillion kilocalories (kcal) of fuel (at both the site of manufacture and embodied in the materials it purchased from other sectors) to produce US$727 million worth of woodworking machinery. There were therefore 426,4 kcal of fuel embodied in each dollar’s worth of woodworking machinery produced in 1979. If a particular industry purchased US$1 million of this type of machinery, the embodied energy of that equipment would be about 4.3 billion kcal.
The economic usefulness of capital tends to diminish as it wears out, requiring increasing amounts of energy to maintain and repair it. Eventually, capital equipment becomes so worn out that it must be discarded altogether. The rate at which capital depreciates or becomes less useful is not constant but depends in part on the rate at which the capital is used to do economic work, the type of work it performs, and the rate at which it is economically efficient to replace. Although a piece of capital continues to degrade even when idle, the rate at which it wears out increases as its rate of doing economic work increases.
Energy analysts often assume that capital degrades at a constant rate and that this rate is caused by, and spread evenly over, each unit produced by a machine. Based on this assumption, one method for estimating the embodied energy in capital used to produce a good or service is to divide the total energy cost of capital used in production by the number or value of goods and services that the capital produces over its lifetime. This ratio is the quantity of embodied energy used to produce one unit of a good or service. Unfortunately this procedure would be difficult or tedious for every piece of capital.
A second method used in most energy analyses assumes that capital is replaced at a more or less constant rate. The monetary value of the capital "used up" or depreciated each year, converted to its energy equivalent, is an estimate of the energy cost of capital.
Human Labor
Some analysts view labor as just another input that has direct and indirect energy costs of production. Households produce and support human labor just as firms produce capital. In doing so households invest energy and other resources to produce and maintain labor in its economic role. Therefore, labor also has an energy cost associated with its use. These energy costs can be separated into three components: (1) the caloric value of the food the worker consumes; (2) the embodied energy of that food (i.e., the direct plus indirect fuel used to produce food); and (3) the fuel purchased with the wages and salaries of labor. Obviously, there are important differences between human labor and other factors, but this does not alter the fact that labor requires a continuous input of energy to sustain itself.
The biological energy equivalent of labor is the fuel burned when human labor does mechanical work. This quantity of fuel can be measured directly by a respirometer, a device that measures the rate at which oxygen is combined with food to produce carbon dioxide and work. The amount of fuel used depends in part on the type of work being done. For example, a person doing desk work uses about 71 kcal/hr whereas a manual laborer uses about twice that quantity.
A comprehensive analysis of the energy equivalent of labor would include the economic energy required to grow the food metabolized by the worker. The U.S food system uses large amounts of fossil fuels and electricity to grow, harvest, transport, market and prepare food. Based on this use of fuel, the embodied energy cost of food used by human labor could be estimated as the quantity of fuel used to grow and distribute the amount of food consumed by each person: 1354 kcal/hr based on the average American’s diet of 3400 kcal/day in 1980. Some methods for energy cost accounting have used this biological measure as the energy equivalent of human labor.
A still more comprehensive assessment of the energy cost of labor would account for all the direct and indirect uses of fuel that are used to produce the goods and services a worker buys with his or her paycheck. This is a measure of the energy cost of producing and maintaining labor in the household sector. This method overestimates the energy cost of labor because it assumes that all the energy used to support a laborer’s paycheck is necessary to produce and maintain the laborer in his or her economic role. Certainly there is a portion of almost everyone’s income that, if taken away, would not reduce his or her ability to perform on the job (although it would certainly make the laborer less well off). Equally as certain, however, a portion of wages and salaries exists beyond that required for basic needs (food, shelter, clothing) that, if removed, would diminish a laborer’s economic performance. For example, a business woman must receive a salary sufficient to cover the costs of food, shelter, and clothing for her and her family to survive. She also needs enough income to purchase transportation to and from her job. She may also subscribe to several journals in order to stay abreast of advances in her particular field. The reader can see that the list could be expanded substantially.
Suffice it to say that a portion, and probably a substantial portion, of the energy represented by a laborer’s paycheck is a necessary and unavoidable energy cost of producing labor. And, as most businesses recognize, if skilled labor is to be secured for one’s own business, competitive wages must be paid, requiring a substantial portion of the nation’s total energy resource toward giving meaning to those paychecks.
When calculating the energy costs of goods and services, the energy cost of labor should not include all the fuel and nonfuel goods and services bought by a worker’s paycheck because hiring a new worker does not always create new demands for goods and services. It may instead only increase existing demand—that is, people buy fuel and nonfuel goods and services whether they are employed or not. The impact of a new worker on the demand for fuel, which is implicit in the demand for goods, can be estimated by examining the energy used to support an employed laborer versus an unemployed laborer. For example, in 1979 the median income of families in the United States with one employed wage earner was $15,607, whereas the median income of $7648 for households with no wage earner was 49% less. Although the percentage of income spent on direct versus indirect purchases of fuel varies with income, a rough approximation is that the employed earner used about 51% more fuel and bought 51% more goods and services than did an unemployed laborer. Based on this assumption the energy cost to society of having an average new laborer can be estimated as 51% of the fuel represented by all dollar purchases of that employed laborer. Since some new jobs are filled not by unemployed workers but by individuals who change jobs, the estimate for the energy equivalent of labor must be corrected for employment levels.
Some analysts have argued that labor should not be assigned an energy cost, while others argue that like all factors of production, labor has energy costs associated with its production and maintenance which need to be included in net energy analysis. The difficulty centers in part on what portion of the total energy used by labor should be included as an energy cost. Should the energy equivalent of a laborer’s entire paycheck be included, or just that portion necessary to support labor in its economic role? If one chooses the latter option, then what energy use by labor is "necessary" to maintain labor as a factor of production? Such decisions are arbitrary and can produce very large differences in estimates of the energy costs of goods or services.
By modifying the models used by Bullard and Herendeen, Costanza calculated the energy costs of goods and services in the U.S. with an estimate of the energy cost of labor and government services. The energy costs of goods increase substantially because Costanza’s model allocates the energy equivalent of labor’s entire income to goods produced by labor. To calculate the energy costs of labor, Costanza modified the boundaries of the input-output model used by Bullard and Herendeen to include labor and government energy costs. Consumption of gross national product (GNP) by households was assumed to be a necessary cost of producing and maintaining labor as a factor of production. In GNP accounting terms, the energy equivalent of personal consumption expenditures represent the energy cost of labor. With labor and government made endogenous to the input-output model, the only major output of Costanza’s revised "economy" was gross capital formation. Although it was not explicitly stated, an underlying assumption made by Costanza was that the primary "purpose" of economic activity was to increase capital stocks. This is quite a different assumption from the conventional definition of GNP which has consumption expenditures, government services and net exports as outputs as well as investment. Because of the different value judgments used to define system boundaries, Costanza’s estimates of the energy costs of goods and services are not directly comparable to energy intensities calculated using conventional GNP definitions. Although labor does have energy costs associated with it, Costanza’s method overestimates those costs by counting all of labors’ income as an energy cost. More importantly, his calculations are derived from a model of the economy that is radically different than the one which generates most economic data.
Environmental Services
Most energy analysts ignore the energy costs of environmental services used in the energy supply process. In this regard energy analysis fares no better than economic analysis. Herendeen argued that the theory and techniques to estimate the energy costs of environmental services are not sufficiently developed to stand the test of self-consistency, completeness, and coherence. Net energy analyses which have attempted to incorporate estimates of the energy costs of degraded environmental services have used very aggregated estimates that have errors of unknown type and magnitude.
A notable exception to this is Odum’s eMergy analysis. This method calculates the amount of one type of energy required to produce a heat equivalent of another type of energy. To account for the difference in quality of thermal equivalents among different energies, all energy costs are measured in solar emjoules (SEJ), the quantity of solar energy used to produce another type of energy. Odum’s method is extremely comprehensive in that it attempts to account for every physical flow of energy and material that supports a given economic activity. As such, it attempts to aggregate disparate energy and material flows into single numeraire that indicates the quantity of environmental support associated with economic activity. As we develop below, however, there are serious conceptual and methodological problems that plague eMergy analysis and thereby limit its usefulness as a tool to analyze economy-environment interactions.
Joint Products
The problem of allocating joint costs is as difficult in net energy analysis as it is in economic analysis. The problem is difficult for two jointly produced fuels such as oil and gas, but is even more intractable when a fuel is jointly produced with a non-fuel. For example, uranium is a byproduct of phosphate mining in Florida, and the conversion of shale oil to a liquid fuel also produces sulfur and ammonia. The net energy analyst is thus confronted with choosing a system to allocate jointly incurred costs amongst various joint products. Any joint cost allocation scheme, even those based on "reasonable" assumptions about the system in question, is ultimately arbitrary, and the choice of allocation methods can have significant impacts on EROI calculations. For example, ethanol production from grain produces crop residues as a byproduct of the harvesting process, and a feed byproduct in the distillation stage. The crop residues are potential fuel source, and the feed byproduct can be used as a fuel or as a foodstuff for cattle. Chambers et al. showed that the EROI for ethanol production was sensitive to the method used to allocate joint costs.
A variety of joint cost allocation schemes have been proposed by energy analysts:
- Assign all energy costs to the principal output.
- Assign energy costs so that each product has the same energy cost per dollar value.
- Assign energy costs on a weight basis so each product has the same energy cost per ton.
- Assign energy costs on a calorific basis so each product has the same energy cost per BTU.
The first method is the easiest and embodies a strong value judgment about the purpose of the process, for example that crude oil is much more valuable to the firm or to the society than natural gas and therefore should be assigned all production costs. The second method is dangerous because prices change frequently over time and may be different to different users of energy. Allocation by weights is attractive because it is physically based, but could lead to the illogical result of an energy cost of a product being less than its true calorific value.
Chapman et al. argued that allocation according to the enthalpies of the byproducts is the only "physically sensible" approach. Leach, however, noted that this method is not suitable in the case of fuel and nonfuel byproducts such as uranium and phosphate. When applied to the joint production of oil and gas, this approach assumes that a BTU of crude oil requires the same amount of energy to lift as natural gas. By its nature, however, natural gas is much less energy-intensive to lift than a liquid such as crude oil, and in certain circumstances provides energy to help lift oil out of a reservoir. In the EROI model developed in the next chapter, an alternative method of allocating joint oil and gas production costs will be developed based on such physical differences.
Energy Discounting
Is a BTU of crude oil extracted today worth the same to society as a BTU produced 10 years from today? The heating value of oil would be the same, but it is possible that its economic usefulness will change as a function of a variety of economic, social, institutional, and technological factors. Critics of net energy analysis have charged that net energy analysis is not a useful policy tool because it assumes that all BTU’s produced or conserved over time have the same utility to society. Such critics have argued that people prefer present use of energy over future use in a manner similar to the way they are assumed to discount dollar values. A frequently cited example of this problem is the use of the energy payback period in which the quantity calculated is the length of time an energy system (e.g., a power plant) takes to produce as much energy as was required for that system’s construction. By not discounting energy costs and benefits, some net energy analysts have assumed that society is indifferent between two facilities that have equivalent EROI’s, but one facility pays back its energy costs in the first few years while the other takes ten years.
Since there is no a priori reason to believe that users of energy don’t discount energy like they discount dollars, certain types of net energy analyses may be justifiably criticized for not addressing the issue of discounting. On the other hand, if future alternative fuels are of lower quality than petroleum, the last barrels of petroleum produced may be more valuable than those currently being used. It should be noted, however, that despite its widespread use, there is not a consensus amongst economists about what the appropriate discount is, or if discounting nonrenewable resources maximizes the rate of resource use in the present at the expense of the welfare of future generations.
Hannon employed a standard continuous discounting function in EROI calculations for various energy systems. Hannon defined that discount rate as the mechanism by which society implicitly expresses its desire to convert a present surplus of energy into an energy supply process to insure future supplies of that energy, rather than consuming that energy now for purposes such as home heating and leisure living. Hannon found that different energy systems had different discount factors associated with them. Not surprisingly, using an energy discount rate in EROI calculations had the largest impact on energy systems such as nuclear power and the solar-powered satellite which require large capital (and hence indirect energy) outlay before energy delivery begins.
Methods of Energy Cost Accounting
There are two general methods of calculating the embodied energy cost of goods and services: process analysis and input-output analysis. Both process and input-output analyses condense the use of energy in production into two general types: fuel burned at the site of energy extraction (direct fuel use), and fuel burned in other sectors to produce the materials purchased and used as inputs at the site of extraction (indirect fuel use). Process analysis and energy input-output analysis, and variants of each, differ in the way the flow of material is traced through the extraction process, the types of energy costs included in the analysis (e.g., just fuel, or fuel, capital, and labor), and the energy equivalents assigned to the three factors of production. As a result, the methods give somewhat different values for embodied energy even when applied to the same set of data.
Process Analysis
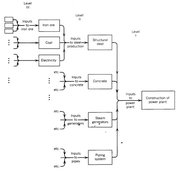
In theory, process analysis provides the most detailed information on the energy cost of goods and services. There are several practical problems, however, such as data limitations, that effectively limit its applicability. Process analysis assesses the energy used directly in each successive step of the production of a good or service. Depending on the data available, energy requirements may be calculated per unit mass or per dollar value of the input. Consider Figure 2, which depicts schematically how the energy cost of producing a power plant might be calculated by the process analysis approach. The same general format would apply to any energy system.
Direct energy costs of a power plant refer to the fuel burned at the site of production—diesel fuel burned by cement trucks, electricity and gas used by welders, and so on. Indirect energy costs are those incurred in the production of the steel, cement, and other raw materials. Going one step further, indirect energy costs also include the energy used to make the structural steel and mine the iron ore used to build the power plant. This leads to one of the problems with process energy analysis, namely, where does one draw the system boundary? This is referred to as the truncation problem because there is no standard procedure for determining when energy costs become small enough to neglect.
Energy Input-Output Analysis
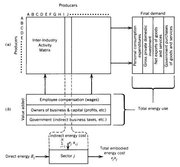
The energy input-output approach is more comprehensive than process analysis and is analogous to and derived from the input-output matrix used in standard economic analyses. Herendeen and Bullard, Hannon et al., and others at the Energy Research Group the University of Illinois modified the economic input-output tables that are based on dollar flows to energy input-output tables based on embodied energy flows between industries. The input-output table breaks the economy into about 400 different sectors. The numbers in the table represent the quantity of direct plus indirect energy that each industry purchases from all other sectors in order to manufacture its product. Combined with the dollar flows between industries, the energy intensity factor (Btu/$) of each good service can be calculated (see Figure 3). These results give a comprehensive and reasonably accurate representation of both the direct and indirect energies used to manufacture a product. The input-output approach does not suffer from the truncation problem of process analysis.
Hall et al. modified the energy input-output analysis so that they did not need to specify the specific upstream sector(s) from which a sect producing final goods purchased materials. Instead, their method is based on a very aggregated estimate of the energy embodied in the intermediate goods at the site of final manufacture.
Costanza modified the boundaries of the traditional input-output tables so that fuel energy (including solar energy) would be the only net input to the economy, with labor and government classified as internal transactions within the economic system and gross capital formation as the principal output. Costanza estimated the quantity of fuel energy used to support labor and government services—as well as that used directly for production—and divided this amount of fuel use by employee compensation and indirect business taxes to estimate the energy used to support a dollar’s worth of labor and government service, respectively. Double counting was avoided by constraining the analysis to use only actual total energy use. In other words the energy used directly by labor was included, but not the energy embodied in goods and services purchased by labor.
Energy Aggregation and Energy Quality
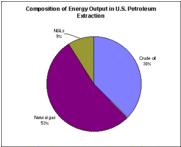
The calculation of the EROI and its variants reflects the desire to arrive at a single number for a system’s performance. But to do so the analyst must add up and compare many different forms of energy. For example an energy system such as petroleum extraction yields three different forms of energy: crude oil, natural gas, and natural gas liquids. Figure 4 demonstrates this for petroleum extraction in the U.S. in 1997. In turn, the extraction process is powered by a range of fuels: gasoline, distillate and residual fuels, natural gas, electricity and small amounts of other fuels (see Figure 5).
When measured in thermal units, crude oil accounts for 38 percent of energy extraction, yet oil products account for just 15 percent of energy used in the extraction industry. Furthermore, the oil products used in the extraction process (gasoline, distillate and residual fuels) have been refined, making them qualitatively very different from crude oil. Another important difference is that electricity and coal are used in extraction, but are absent from the outputs of extraction.
This raises a critical question in energy analysis: how does one aggregate forms of energy with disparate attributes? The simplest and most common form of aggregation, is addition by thermal equivalents (BTUs, joules etc):
- :: ::: :::: ::::: :::::: ::::::: :::::::: :::::::::
where E represents the thermal equivalent of fuel i (N types) at time t. The advantage of the thermal equivalent approach is that it uses a simple and well-defined accounting system based on the conservation of energy, and the fact that thermal equivalents are easily and uncontroversially measured. This approach underlies most methods of energy aggregation in economics and ecology, such as trophic dynamics, national energy accounting, energy input-output modeling in economies and ecosystems, most analyses of the energy/GDP relationship and energy efficiency, and most net energy analyses.
Defining Energy Quality
Despite its widespread use, aggregating different energy types by their heat units embodies a serious flaw: it ignores qualitative differences among energy vectors. Defined by Kaufmann and Cleveland et al, energy quality is the relative economic usefulness per heat equivalent unit of different fuels and electricity. Thus, the essence of energy quality is not derived entirely from a fuel’s physical, thermodynamic or engineering attributes, nor entirely by people’s preferences as expressed in the market. Rather, the quality of energy is defined by at the nexus of how a fuel’s physical, thermodynamic or engineering attributes affect its usefulness to people, and, in turn, how people value the services derived from the use of energy.
Schurr and Netschert were among the first to recognize the economic importance of energy quality. Noting that the composition of energy use changes significantly over time, Schurr and Netschert argue that the general shift to higher quality fuels affects how much energy is required to produce gross national product (GNP). The quality of electricity has received considerable attention in terms of its effect on the productivity of labor and capital and on the quantity of energy required to produce a unit of GDP. Less attention has been paid to the quality of other fuels, and few studies use a quality-weighting scheme in empirical analysis of energy use.
Taking energy quality into account in energy aggregation requires more advanced forms of aggregation. Some of these forms are based on concepts developed in the energy analysis literature such as exergy or emergy analysis. These methods take the following form:
- :: ::: :::: ::::: :::::: ::::::: :::::::: ::::::::: :::::::::: :::::::::::
where the &lambda’s are quality factors that may vary among fuels and over time for individual fuels. In the most general case, an aggregate index can be represented as:
- :: ::: :::: ::::: :::::: ::::::: :::::::: ::::::::: :::::::::: :::::::::::
where f() and g() are functions, ?it are weights, the Ei are the N different energy vectors and Et is the aggregate energy index in period t. An example of this type of indexing is the discrete Divisia Index or Tornquist-Theil Index described below.
Economic Approaches to Energy Quality
From an economic perspective, the value of a heat equivalent of fuel is determined by its price. Price-taking consumers and producers set marginal utilities and products of the different energy vectors equal to their market prices. These prices and their marginal productivities and utilities are set simultaneously in general equilibrium. The value marginal product of a fuel in production is the marginal increase in the quantity of a good or service produced by the use of one additional heat unit of fuel multiplied by the price of that good or service. We can also think of the value of the marginal product of a fuel in household production.
The marginal product of a fuel is determined in part by a complex set of attributes unique to each fuel such as physical scarcity, capacity to do useful work, energy density, cleanliness, amenability to storage, safety, flexibility of use, cost of conversion, and so on. But the marginal product is not uniquely fixed by these attributes. Rather, the energy vector’s marginal product varies according to the activities in which it is used, how much and what form of capital, labor, and materials it is used in conjunction with, and how much energy is used in each application. As the price rises due to changes on the supply-side, users can reduce their use of that form of energy in each activity, increase the amount and sophistication of capital or labor used in conjunction with the fuel, or stop using that form of energy for lower value activities. All these actions raise the marginal productivity of the fuel. When capital stocks have to be adjusted, this response may be somewhat sluggish and lead to lags between price changes and changes in the value marginal product.
The heat equivalent of a fuel is just one of the attributes of the fuel and ignores the context in which the fuel is used, and thus cannot explain, for example, why a thermal equivalent of oil is more useful in many tasks than is a heat equivalent of coal. In addition to attributes of the fuel, marginal product also depends on the state of technology, the level of other inputs, and other factors. According to neoclassical theory, the price per heat equivalent of fuel should equal its value marginal product, and, therefore, represent its economic usefulness. In theory, the market price of a fuel reflects the myriad factors that determine the economic usefulness of a fuel from the perspective of the end-user.
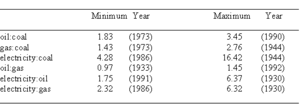
Consistent with this perspective, the price per heat equivalent of fuel varies substantially among fuel types (see Table 1). The different prices demonstrate that end-users are concerned with attributes other than heat content. As Berndt, 1978, stated:
Because of the variation in attributes among energy types, the various fuels and electricity are less than perfectly substitutable - either in production or consumption. For example, from the point of view of the end-user, a Btu of coal is not perfectly substitutable with a Btu of electricity; since the electricity is cleaner, lighter, and of higher quality, most end-users are willing to pay a premium price per Btu of electricity. However, coal and electricity are substitutable to a limited extent, since if the premium price for electricity were too high, a substantial number of industrial users might switch to coal. Alternatively, if only heat content mattered and if all energy types were then perfectly substitutable, the market would tend to price all energy types at the same price per Btu.
Do market signals (i.e., prices) accurately reflect the marginal product of inputs? Kaufmann investigates this question in an empirical analysis of the relation between relative marginal product and price in U. S. energy markets. To do so, he estimates a reduced form of a production function that represents how the fraction of total energy use from coal, oil, natural gas, and primary electricity (electricity from hydro and nuclear sources) affects the quantity of energy required to produce a given level of output. The partial derivatives of the production function with respect to each of the fuels gives the marginal product of individual fuels, in which marginal product is defined as the change in economic output given a change in the use of a heat unit of an individual fuel. The equations are used to calculate the marginal product for each fuel type for each year between 1955 and 1992. The time series for marginal products are compared among fuels, and these ratios are related to relative prices using a partial adjustment model. The results indicate that there is a long run relation between relative marginal product and relative price, and that several years of adjustment are needed to bring this relation into equilibrium. The results are summarized in Table 2, and suggest that over time, prices do reflect the marginal product—and hence the economic usefulness—of fuels.
Other analysts calculate the average product of fuels, which is a close proxy for marginal products. Adams and Miovic estimate a pooled annual cross-sectional regression model of industrial output as a function of fuel use in seven European economies from 1950 to 1962. Their results indicate that petroleum is 1.6 to 2.7 times more productive than coal in producing industrial output. Electricity is 2.7 to 14.3 times more productive than coal. Using a regression model of the energy/GDP ratio in the U.S., Cleveland et al. find that the quality factors of petroleum and electricity relative to coal were 1.9 and 18.3, respectively.
Price-Based Aggregation
If marginal product is related to its price, energy quality can be measured by using the price of fuels to weight their heat equivalents. The simplest approach defines the weighting factor (?’s) as:
- :: ::: :::: ::::: :::::: ::::::: :::::::: ::::::::: :::::::::: :::::::::::
where Pit is the price per Btu of fuel. In this case, the price of each fuel is measured relative to the price of fuel type 1. Turvey and Nobay use equation (4) to aggregate fuel use in the UK.
The quality index in equation (4) equation embodies a restrictive assumption that fuels are perfect substitutes and the index is sensitive to the choice of numeraire. Because fuels are not perfect substitutes, a rise in the price of one fuel relative to the price of output will not be matched by equal changes in the prices of the other fuels relative to the price of output. For example, the rise in oil prices in 1979-80 would cause an aggregate energy index which uses oil as the numeraire to fall dramatically. An index that uses coal as the numeraire would show a large fall in 1968-74, one not indicated by the oil-based index.
To avoid dependence on a numeraire, Berndt proposed a discrete approximation to the Divisia index to aggregate energy. The formula for constructing the discrete Divisia index E* is:
- :: ::: :::: ::::: :::::: ::::::: :::::::: ::::::::: :::::::::: ::::::::::: :::::::::::: ::::::::::::: :::::::::::::: ::::::::::::::: ::::::::::::::::
where P are the prices of the n fuels,and E are the quantities of BTU for each fuel in final energy use. Note that prices enter the Divisia index via cost or expenditure shares. The Divisia index permits variable substitution among material types without imposing a priori restrictions on the degree of substitution. Diewert shows that this index is an exact index number representation of the linear homogeneous translog production function where fuels are homothetically weakly separable as a group from the other factors of production. With reference to equation (3), f() = g() = ?ln(), while ?it is given by the average cost share over the two periods of the differencing operation.
Aggregation using price has its shortcomings. Lau suggests that prices provide a reasonable method of aggregation if the aggregate cost function is homothetically separable in the raw material input prices. This means that the elasticity of substitution between different fuels is not a function of the quantities of non-fuel inputs used. This may be an unrealistic assumption in some cases. Also, the Divisia index assumes that the substitution possibilities among all fuel types and output are equal.
It is well-known that energy prices do not reflect their full social cost due to a number of market imperfections. This is particularly true for the environmental impact caused by their extraction and use. These problems lead some to doubt the usefulness of price as the basis for any indicator of sustainability. But with or without externalities, prices should reflect productivities. Internalizing externalities will shift energy use, which, in turn, will then change marginal products.
Moreover, prices produce a ranking of fuels (see Table 3) that is consistent with our intuition and with previous empirical research. One can conclude that government policy, regulations, cartels and externalities explain some of the price differentials among fuels, but certainly not the substantial ranges that exist. More fundamentally, price differentials are explained by differences in attributes such as physical scarcity, capacity to do useful work, energy density, cleanliness, amenability to storage, safety, flexibility of use, cost of conversion, and so on. Wipe away the market imperfections and the price per BTU of different energies would vary due to the different combinations of attributes that determine their economic usefulness. The different prices per BTU indicate that users are interested in attributes other than heat content.
The eMergy Approach to Aggregation
Odum and his colleagues analyze energy and materials with a system that traces their flows within and between society and the environment. It is important to differentiate between two aspects of Odum’s contribution. The first is his development of a biophysically-based, systems-oriented model of the relationship between society and the environment. Here Odum’s early contributions helped lay the foundation for the biophysical analysis of energy and material flows, an area of research that forms part of the intellectual backbone of ecological economics. The insight from this part of Odum’s work is illustrated by the fact that ideas he emphasized—energy and material flows, feedbacks, hierarchies, thresholds, time lags—are key concepts of the analysis of sustainability in a variety of disciplines.
The second aspect of Odum’s work, which we are concerned with here, is a specific empirical issue: the identification, measurement, and aggregation of energy inputs to the economy. Emergy (with an "m") analysis is a pure cost-of-production approach that measures the quality of a particular type of energy by its transformity. Transformity is the amount of one type of energy required to produce a heat equivalent of another type of energy. To account for the difference in quality of thermal equivalents among different energies, all energy costs are measured in solar emjoules (SEJ), the quantity of solar energy used to produce another type of energy. According to Odum, fuels with higher transformities require larger amounts of sunlight for their production and therefore are more economically useful.
Odum’s method of calculating transformities assesses the efficiency of the sequence of energy conversions that produce a thermal equivalent of fuel. That sequence has two components: environmental energy conversions and industrial energy conversions. The basis for these calculations is the production of electricity in a wood-fired power plant. The principal environmental energy conversion is the solar energy required to produce a heat equivalent of wood in the standing stock of the forest: 3.23*104 solar emjoules (SEJ) of sunlight are required to produce one joule of standing wood. The sunlight embodied in the wood undergoes a series of energy conversions in the economy (harvest, transport, combustion, etc.) that generate a joule of electricity. The generation of each heat unit of electricity requires 1.59*105 SEJ. The transformities for coal, oil, and natural gas are based on a series of calculations that assess the efficiency of converting coal to electricity, crude oil to refined fuel, and the efficiency of coal relative to natural gas as a boiler fuel.
This approach raises a fundamental question about the appropriateness of transformities to reflect energy quality: Is the usefulness of a fuel as an input to production related to its transformity? Probably not. Users value coal based on it heat content, sulfur content, cost of transportation and other factors that form the complex set of attributes that determine its usefulness relative to other fuels. It is hard to imagine how this set of attributes is in general related to—much less determined by—the amount of embodied emergy. Similarly, any differences in the economically useful attributes of coals laid down 500 or 100 million years ago are not determined by the enormous differences in their embodied emergies. Thus, while Odum’s method provides a useful framework for highlighting he important role the environment plays in generating energy and material resources, it is of dubious value in comparing and aggregating energy flows in economic applications.
In addition to this conceptual issue, there are computational problems with emergy analysis that make transformities incomplete indicators of energy quality. The calculation and application of transformities are time, location, and technology specific, yet Odum and his colleagues mix the temporal, spatial, and technical scales of their analysis in ways that are poorly defined. First, Odum presents the transformities as constants, but based on the method used to calculate them, the transformities are clearly dynamic because they are based on the first law efficiency of technologies such as power plants, coal liquefaction, and oil refineries. The efficiency of those technologies have changed dramatically over time. Second, the emergy calculations also contain an ad hoc mixture of spatial scales. The basis for the calculation of the transformities is the thermal efficiency of a wood-fired power plant in Brazil, but the efficiency of power plants vary throughout the world as do all the other energy conversion technologies used in the emergy calculations. Similarly, energy/output data from the New Zealand economy are mixed with the Brazil power plant data to calculate the transformities, which are then applied to many other economies throughout the world. Third, the values of the transformities are highly sensitive to technological assumptions made by Odum and Odum. They calculate the relative quality of oil, gas, and coal based in part on the fact that the first law thermal efficiency of converting natural gas in [[boiler]s] is 20 percent more efficient than the conversion of coal. However, the relative thermal efficiency of fuels varies with the task they perform. The transformities would change, and hence the estimate of relative fuel qualities, if a different task were used for comparing the thermal efficiency of fuel conversion.
The Exergy Approach to Aggregation
Exergy analysis is based on the second law of thermodynamics that describes the change in the quality of energy that accompanies its conversion from one form to another. Exergy therefore accounts for physical quality differences among different forms of energy. Exergy is the maximum amount of physical work that can be extracted from a given flow of energy. Exergy is calculated by multiplying the heat equivalent of a fuel or heat source by the appropriate Carnot factor [1-(Ta/To)], where Ta and To are the ambient temperature and output temperature of the process, respectively, measured on the Kelvin scale. Note that energy quality in exergy analysis is defined in concise thermodynamic terms: the potential to do mechanical work. Mechanical drive and electricity are rated the highest in the exergy hierarchy of energy quality because of the theoretical capacity of those sources to be transformed into useful work with 100 percent efficiency. The exergy approach accounts for the important reduction in quality (ability to do work) that accompanies the conversion of energy from one form to another, and is typically applied to individual processes or technologies.
Ayres et al. and Ayres and Martiñas propose a system of aggregating energy and materials based on exergy. Exergy measures the useful work obtainable from an energy source or material, and is based on the chemical energy embodied in the material or energy based on its physical organization relative to a reference state. Thus, exergy measures the degree to which a material is organized relative a random assemblage of material found at an average concentration in the Earth's crust, ocean or atmosphere. The higher the degree of concentration, the higher the exergy content. The physical units for exergy are the same as for energy or heat, namely kilocalories, joules, BTUs, etc. For fossil fuels, exergy is nearly equivalent to the standard heat of combustion; for other materials specific calculations are needed that depend on the details of the assumed conversion process.
Ayres argues that exergy has a number of useful attributes for aggregating heterogeneous energy and materials. Exergy is a property of all energy and materials and in principle can be calculated from information in handbooks of chemistry and physics and secondary studies. Thus, exergy can be used to measure and aggregate natural resource inputs as well as wastes. For these reasons, Ayres argues that exergy forms the basis for a comprehensive resource accounting framework that could "provide policy-makers with a valuable set of indicators." One such indicator is a general measure of "technical efficiency," the efficiency with which "raw" exergy from animals or inanimate source is converted into final services. A low exergy efficiency implies potential for efficiency gains for converting energy and materials into goods and services. Similarly, the ratio of exergy embodied in material wastes to exergy embodied in resource inputs is, according to Ayres et al, the "most general measure of pollution". Ayres and Martiñas also argue that the exergy of waste streams is a proxy for their potential ecotoxicity or harm to the environment, at least in general terms.
Cleveland and Herendeen used exergy in their EROI calculations for solar parabolic trough energy systems, which produce heat at temperatures ranging from 50° to 350° C. A standard EROI calculation treats heat produced at the lower temperature as qualitatively the same as heat at higher temperatures, despite the fact that higher temperature heat has greater potential to do work. Cleveland and Herendeen corrected for this quality difference by multiplying the EROI by a Carnot factor which incorporates thermodynamic quality. While the correction procedure was crude, it did demonstrate how fuel quality differences can be incorporated into an EROI analysis.
From an accounting perspective, exergy is appealing because it is based on the science and laws of [[thermodynamic]s] and thus has a well-established system of concepts, rules, and information that are available widely. But like enthalpy, exergy should not be used to aggregate energy and material inputs aggregation because it is one-dimensional. Like enthalpy, exergy does not vary with, and hence does not necessarily reflect attributes of fuels that determine their economic usefulness, such as energy density, cleanliness, cost of conversion, and so on. The same is true for materials. Exergy cannot explain, for example, impact resistance, heat resistance, corrosion resistance, stiffness, space maintenance, conductivity, strength, ductility, or other properties of metals that determine their usefulness. Like prices, exergy does not reflect all the environmental costs of fuel use. The exergy of coal, for example, does not reflect coal’s contribution to global warming or its impact on human health relative to say natural gas. As Ayres himself notes, the exergy of wastes is at best a rough first-order approximation of environmental impact because it does not vary with the specific attributes of a waste material and its receiving environment that cause harm to organisms or that disrupt biogeochemical cycles. In theory exergy can be calculated for any energy or material, but in practice, the task of assessing the hundreds (thousands?) of primary and intermediate energy and material flows in an economy is daunting.
To summarize, emergy and exergy are not appropriate to aggregate energy in an economic analysis because they are one-dimensional. Like enthalpy, exergy and emergy do not vary with, and hence do not necessarily reflect attributes of fuels that determine their economic usefulness, such as energy density, cleanliness, cost of conversion, and so on.