Second Law of Thermodynamics
Second law of thermodynamics
One of three laws of thermodynamics, the Second Law of Thermodynamics is an equation that describes a property of a system known as entropy increases over time.
Thermodynamics is a branch of physics which deals with the energy and work of a system. Thermodynamics deals only with the large scale response of a system which we can observe and measure in experiments. In aerodynamics, the thermodynamics of a gas obviously plays an important role in the analysis of propulsion systems but also in the understanding of high speed flows. The [[size="2" face="Arial, Helvetica, sans-serif">First law of thermodynamics|first law of thermodynamics]]] defines the relationship between the various forms of energy present in a system ([[size="2" face="Arial, Helvetica, sans-serif">Kinetic energy|kinetic]]] and [[size="2" face="Arial, Helvetica, sans-serif">Potential energy|potential]]]), the work which the system performs and the transfer of heat. The first law states that energy is conserved in all thermodynamic processes.
We can imagine thermodynamic processes which conserve energy but which never occur in nature. For example, if we bring a hot object into contact with a cold object, we observe that the hot object cools down and the cold object heats up until an equilibrium is reached. The transfer of heat goes from the hot object to the cold object. We can imagine a system, however, in which the heat is instead transferred from the cold object to the hot object, and such a system does not violate the first law of thermodynamics. The cold object gets colder and the hot object gets hotter, but energy is conserved. Obviously we don't encounter such a system in nature and to explain this and similar observations, thermodynamicists proposed a second law of thermodynamics. Clasius], Kelvin], and Carnot] proposed various forms of the second law to describe the particular physics problem that each was studying.
Entropy has a variety of physical interpretations, including the statistical disorder of the system, but for our purposes, let us consider entropy to be just another property of the system, like enthalpy or temperature.
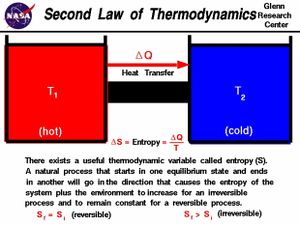
The second law states that there exists a useful state variable called entropy S. The change in entropy?S is equal to the heat transfer?Q divided by the temperature T.
?S =?Q / T
For a given physical process, the combined entropy of the system and the environment remains a constant if the process can be reversed. If we denote the initial and final states of the system by "i" and "f":
Sf = Si (reversible process)
An example of a reversible process is ideally forcing a flow through a constricted pipe. Ideal means no boundary layer losses. As the flow moves through the constriction, the pressure, temperature and velocity change, but these variables return to their original values downstream of the constriction. The state of the gas returns to its original conditions and the change of entropy of the system is zero. Engineers call such a process an isentropic process. Isentropic means constant entropy.
The second law states that if the physical process is irreversible, the combined entropy of the system and the environment must increase. The final entropy must be greater than the initial entropy for an irreversible process:
Sf > Si (irreversible process)
An example of an irreversible process is the problem discussed in the second paragraph. A hot object is put in contact with a cold object. Eventually, they both achieve the same equilibrium temperature. If we then separate the objects they remain at the equilibrium temperature and do not naturally return to their original temperatures. The process of bringing them to the same temperature is irreversible.