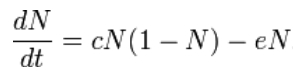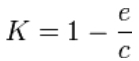Metapopulation
A species metapopulation is defined as a set of spatially separated populations, which have some form of migration or mixing behavior among them. Animal populations are often thought of in the context of metapopulations, but plants are an equally worthy subject, since seed dispersal is tantamount to animal migration in connecting disparate habitat patches. The name metapopulation was first used in 1970 by Levins to describe a population dynamics model for insect pests inhabiting crop growing areas; however, the idea has since been most broadly applied to species in fragmented habitats.
Contents
Concept description
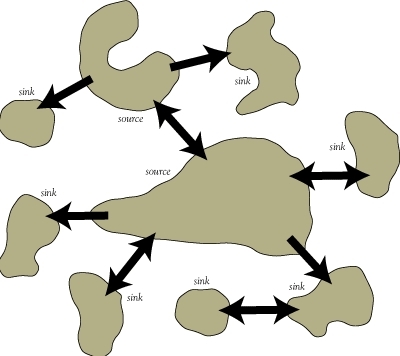
A metapopulation construct is normally considered to consist of several spatially discrete populations, along with areas of suitable habitat which are either occupied or unoccupied. In classical metapopulation theory, each population progresses relatively decoupled from the other populations, and ultimately is extirpated as a consequence of demographic stochasticity (fluctuations in population size due to ostensibly random demographic events); the smaller the population, the more likely it resides in an extinction vortex (path of relatively imminent extinction). There is an analog to gambler's ruin, which is a mathematical probabilistic theory that any individual gambler with finite assets will lose all of his money, when playing against the house.
Although individual populations exhibit finite lifespans, the metapopulation as a whole is often stable because immigrants from one population (which may, for example, be undergoing a population boom) are likely to re-colonize habitat which has been vacated by the local extinction of a second population. They may also emigrate to enlarge a small population and rescue that population from extinction (called the rescue effect). The development of metapopulation theory, in conjunction with the development of source-sink dynamics, emphasizes the significance of connectivity between apparently isolated populations. Although no single population may be able to insure the long-term survival of a given species, the combined effect of many populations may be able to achieve a successful outcome.
Predator-prey cycles
 Painted hunting dog, Okavango Delta, Botswana
Painted hunting dog, Okavango Delta, Botswana
@ C.Michael Hogan
Some early experiments with predation and spatial heterogeneity were conducted by Georgii Gause in the 1930s, based on the Lotka-Volterra equation, which was first developed in the mid-1920s, without experimental confirmation until Gause.The Lotka-Volterra equation suggested that the relationship between predators and their prey would result in population oscillations over time based on the initial densities of predator and prey (Predator-prey cycles). Gause's early experiments to prove the predicted oscillations of this theory failed because the predator-prey interactions were not influenced by immigration. However, once immigration was introduced, the population cycles accurately depicted the oscillations predicted by the Lotka-Volterra equation, with the peaks in prey abundance shifted slightly to the left of the peaks of the predator densities. Huffaker's experiments expanded on work of Gause by examining how both the factors of migration and spatial heterogeneity lead to predator-prey oscillations.
Examples of metapopulations
There are clear examples of metapopulations at all geographic scales and every region of the Earth. The following are a few specific instances to allow one to envision the great panoply of occurrences:
- Painted hunting dog (Lycaon pictus) is a patchily distributed carnivorous mammal in sub-Saharan Africa. Large primordial semi-continuous populations have been decimated by habitat destruction, habitat fragmentation, extensive poaching and genetic pollution by domesticated canids. As a result the patches are sufficiently severed that rescue effects and stochastic progression has placed this species in a potential extinction vortex.
- Various Caribbean Sea coral reef fishes are distributed in discrete populations based upon their intrinsic affinity for reef habitat preferences. Destruction of many of these reefs from mechanical damage, water pollution and coral bleaching have diminished some of the habitats such that local extirpation of certain reef fishes such as the Nassau grouper.
- Butterfly populations of Jasper Ridge, California have been extensively studied by Paul Ehrlich since the mid 1900s. Examination of the movement, rescue effects, colonization and metapopulation extinction provided Ehrlich much of his insights for his seminal work Extinction.
 Jasper Ridge Biological Preserve, San Francisco Peninsula.
Jasper Ridge Biological Preserve, San Francisco Peninsula.
Huffaker experiments
In order to study predation and population oscillations, Huffaker used mite species, one being the predator and the other being the prey. He set up a controlled experiment using oranges, a food source for the mites, as the spatially structured habitat in which the predator and prey would interact. Initially, Huffaker experienced difficulties similar to those of Gause in creating a stable predator-prey interaction. By using oranges only, the prey species quickly went extinct, followed consequently with predator extinction.
However, Huffaker found that modifying the spatial structure of the habitat allowed manipulation of the population dynamics, increasing the populations of both predator and prey (Predator-prey cycles). He did this by altering the distance between the prey and their food source, establishing barriers to predator movement, and creating artificial Biological corridor for the prey to disperse. These changes resulted in increased habitat patches and in turn provided more areas for the prey to seek temporary protection. When the prey would become extinct locally at one habitat patch, they were able to reestablish by migrating to new patches before being attacked by predators. This habitat spatial structure of patches allowed for coexistence between the predator and prey species and promoted a stable population oscillation structure.
Even though the term metapopulation had not yet been coined, the environmental factors of spatial heterogeneity and habitat patchiness would later describe the conditions of a metapopulation relating to how groups of spatially separated populations of species interact with one another. Huffaker's experiment is significant because it showed how metapopulations can directly affect the predator-prey interactions and in turn influence population dynamics. In spatially structured landscapes, species populations typically exist as metapopulations, which consist of subpopulations each of which inhabits a habitat patch. If individual members of species can move between patches, the outcome is usually favourable for survival of metapopulation because it encourages recolonization of patches.
Levins algorithm
Levins' original model applied to a metapopulation distributed over many patches of suitable habitat with significantly less interaction between patches than within a patch. In the parlance of Levins: this phenomenon is termed a population of populations. Population dynamics within a patch were simplified to the point where only presence and absence were considered. Each patch in his model is either populated or not. Assume N is the fraction of patches occupied at a given time. During a time dt, each occupied patch can become unoccupied with an extinction probability edt. Additionally, 1−N of the patches are unoccupied. Assuming a constant rate c of propagule generation from each of the occupied patches, during incremental time dt, each unoccupied patch becomes occupied with a colonization probability cNdt.
As a result, the time rate of change of occupied patches, dN/dt, is given by:
This rendition is tantamount to the logistic model, with a carrying capacity K given by:
and growth rate alpha:
alpha = c - e.
At equilibrium, therefore, some fraction of the species's habitat will always be unoccupied. Stochasticity and metapopulations Huffaker's analyses of spatial structure and species interactions are an example of early experimentation in metapopulation dynamics. Since the experiments of Huffaker and Levins, models have been created which integrate stochastic factors. These models have proven that the combination of environmental variability (stochastity) and relatively small migration rates induce indefinite or unpredictable persistence.
However, Huffaker's experiment had a built in outcome of guaranteed infinite persistence, due to the controlled immigration variable. Stochastic patch occupancy models One drawback of the Levins model is that it is deterministic, while the fundamental metapopulation processes are more properly considered stochastic. Metapopulations are particularly useful when discussing species in disturbed habitats, and their minimum viable population, i.e., how likely they are to become extinct in a given time interval. Although the Levins approach does not address this matter, a simple way to extend the Levins model adding spatial and stochastic considerations is to invoke the contact process. Further extentiaos of this model can also simulate patch dynamics. At a given percolation threshold, habitat fragmentation effects transpire in these configuration predicting more dramatic extinction thresholds. For conservation biology purposes, metapopulation models must include (a) the finite nature of metapopulations (how many patches are suitable for habitat), and (b) the probabilistic nature of extinction and colonisation. For these models to function effectively, the patch extinctions and colonisations are necessarily asynchronous.
Application to aquatic systems
Metapopulation theory was first developed for terrestrial ecosystems, and only later applied to the marine realm. In fisheries science, the term sub-population is equivalent to the metapopulation science term local population. Most marine examples are provided by relatively sedentary species occupying discrete patches of habitat, with both local recruitment and rescue effect from other local populations of the larger metapopulation assembly. Kritzer and Sale warned against strict application of the metapopulation definitional criteria: that extinction risks to local populations must be non-negligible.
Micro-habitat patches and microchips
By combining nanotechnology with landscape ecology, a habitat landscape can be simulated on a microchip by building a collection of nano-fabricated bacterial habitats, and connecting them by corridors in different topological arrangements, with nano-scale channels providing them with the local ecosystem service of habitat renewal. These landscapes of micro-habitat patches can be utilized as physical implementations of an adaptive landscape by generating a spatial mosaic of patches of opportunity distributed in space and time. The patchy nature of these simulated landscapes enables study of adapting bacterial cells in a metapopulation system operating on-chip within a synthetic ecosystem. The metapopulation biology and evolutionary ecology of these bacterial systems is thus analyzed by applying experimental biophysics. Life stages example Metapopulation models have been used to explain life-history evolution, such as the ecological stability of amphibian metamorphosis in small scale vernal pools. Alternative ecological strategies have evolved. For example, some salamanders forgo metamorphosis, sexually maturing in aquatic neotonic form. The seasonal duration of wetlands and the migratory range of the species determines which ponds are connected, and how the metapopulations are spatially distributed. The duration of the life stages of amphibians relative to the duration of a vernal pool (prior to desiccation) regulates the ecological development of metapopulations connecting aquatic patches to terrestrial patches.
See also
- Population viability analysis
- Causes of extinction
- Extinction vortex
- Habitat fragmentation
- Predator-prey cycles
- Spatial heterogeneity
References
- J.Bascompte and R.V.Solé. 1996. Habitat Fragmentation and Extinction Thresholds in spatialy explicit models . Journal of Animal Ecology. vol. 65. issue 4. pp. 465–473
- I.Hanski. Metapopulation Ecology Oxford University Press. 1999. ISBN 0-19-854065-5
- L.Fahrig. 2003. Effects of Habitat Fragmentation on Biodiversity. Annual Review of ecology, evolution, and systematics. 34:1
- A.Janssen, A. et al. 1997. Metapopulation Dynamics of a Persisting Predator-Prey system. •P.Kareiva. 1987. Habitat Fragmentation and the Stability of Predator-Prey Interactions. Nature vol. 326, issue 6111
- C.B.Huffaker. 1958. Experimental Studies on Predation: Dispersion factors and predator-prey oscillations. Hilgardia. vol. 27 issue 343. 83 pages
- J.E. Keymer, P.A.Marquet, J.X.Velasco?Hernández. 2000. Extinction Thresholds and Metapopulation Persistence in Dynamic Landscapes. The American Naturalist. Vol. 156
- J.P.Kritzer and P.F.Sale (eds) 2006. Marine metapopulations, Academic Press, New York.
- P.Legendre and M.J. Fortin. 1989. Spatial pattern and ecological analysis Plant Ecology. Vol. 80, issue 2
- R.Levins. 1969. Some demographic and genetic consequences of environmental heterogeneity for biological control . Bulletin of the Entomological Society of America. Vol. 15 |pp 237–240
- S.A. Levin. 1974 Dispersion and Population Interactions The American Naturalist. Vol. 108 | issue 960
- J.E.Keymer, P.Galajda, R.Muldoon and R.Austin. 2006. Bacterial metapopulations in nanofabricated landscapes. PNAS vol.103 pp 17290–295
- Dale R. McCullough. 1999. Metapopulations and wildlife conservation. Wildlife Society. Island Press. 429 pages
- Leslie A.Real and James H.Brown. 1991. Foundations of Ecology: Classic papers with commentaries. University of Chicago Press, Chicago, Illinois.