Eddy covariance method
Eddy Covariance (also termed Eddy Correlation, Eddy Flux) technique is an atmospheric flux measurement technique to monitor and calculate vertical turbulent fluxes within atmospheric boundary layers. Such flux measurements are widely used to estimate momentum, heat, water, and carbon dioxide exchange, as well as exchange of methane and other trace gases.
The technique is also used extensively for verification and tuning of global climate models, mesoscale and weather models, complex biogeochemical and ecological models, and remote sensing estimates from satellites and aircraft.
The technique is mathematically complex, and requires a considerable care in gathering and processing data. To date, there is no uniform terminology or a single methodology for the Eddy Covariance technique, but much effort is being made by flux measurement networks (e.g., Fluxnet, Ameriflux, CarboEurope, Fluxnet Canada, and iLEAPS) to unify various approaches.
Contents
General principles
Representation ofthe air flow in the atmospheric boundary layer
Air flow can be envisioned as a horizontal flow of numerous rotating eddies, a turbulent vortices of various sizes, with each eddy having three-dimensional components, including vertical components as well. The situation appears chaotic, but vertical movement of the components can be measured from the tower.
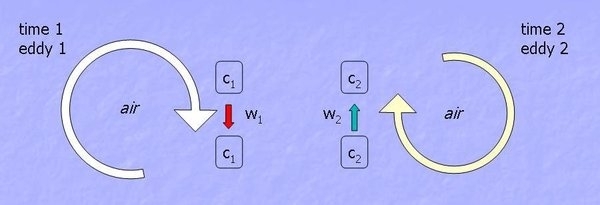
Physical meaning of the Eddy Covariance method
At one physical point on the tower, at Time1, Eddy1 moves parcel of air C1 down at the speed W1. Then, at Time2, Eddy2 moves parcel C2 up at the speed W2. Each parcel has a concentration, temperature, and humidity. If these factors, along with the speed are known, we can determine the flux. For example, if one knew how many molecules of water moved upward with eddies at Time1, and how many molecules moved downward with eddies at Time2, at the same point, one could calculate the vertical flux of water at this point over this time interval.
So, vertical flux can be presented as a covariance of the vertical wind velocity and the concentration of the entity of interest.
Mathematicalfoundation
In mathematical terms,"eddy flux" is computedas a covariance between instantaneous deviation in vertical wind speed (w') from the mean value (w-overbar) and instantaneous deviation ingas concentration, mixing ratio(s'), from its mean value (s-overbar), multiplied bymean air density (ρa). Several mathematical operation and assumptions, including Reynolds decomposition,are involved in getting from physically complete equations of the turbulent flow to a practical equations for computing "eddy flux", as shown below.
Major assumptions
- Measurements at a point can represent an upwind location
- Measurements are conducted inside the boundary layer of interest
- Fetch/flux footprint is adequate – fluxes are measured only at the area of interest
- Flux is fully turbulent – most of the net vertical transfer is carried out by eddies
- Topography is horizontal and uniform: average of fluctuations is zero; density fluctuations negligible; flow convergence and divergence are negligible
- Instruments can detect very small changes athigh frequency, ranging from minimum of 5 Hertz and to 40 Hertz for tower-based measurements
Further reading
- Baldocchi, D., B. Hicks, and T. Meyers. 1988.Measuring biosphere-atmosphere exchanges of biologically related gases with micrometeorological methods. Ecology 69, 1331-1340
- Burba, G., and D.Anderson, D.J. 2007. Introduction to the Eddy Covariance Method: General Guidelines and Conventional Workflow. LI-COR Biosciences, 141 pp
- Lee, X., W. Massman, and B. Law. 2004. Handbook of Micrometeorology. Kluwer Academic Publishers, The Netherlands, 250 pp
- Verma, S.B.: 1990, Micrometeorological methods for measuring surface fluxes of mass and energy, Remote Sensing Reviews 5(1): 99-115.