Spatial reference systems
Spatial coordinates and timing conventions are adopted in order to consistently identify locations and motions of an observer, of natural objects in the solar system, and of spacecraft traversing interplanetary space or orbiting planets or other bodies. Without these conventions it would be impossible to navigate the solar system.
Contents
Terrestrial Coordinates
Figure 1: Longitude Lines (Source: NASA) A great circle is an imaginary circle on the surface of a sphere whose center is the center of the sphere. Great circles that pass through both the north and south poles are called meridians, or lines of longitude (Figure 1). For any point on the surface of Earth a meridian can be defined.
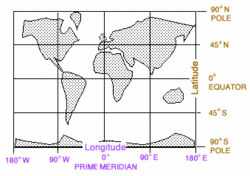Figure 2: Terrestrial Coordinates Grid (Source: NASA) The prime meridian, the starting point measuring the east-west locations of other meridians, marks the site of the old Royal Observatory in Greenwich, England. Longitude is expressed in degrees, minutes, and seconds of arc from 0 to 180 degrees eastward or westward from the prime meridian. For example, downtown Pasadena, California, is located at 118 degrees, 8 minutes, 41 seconds of arc west of the prime meridian: 118° 8' 41" W.
Figure 3: Latitude Lines (Source: NASA) The starting point for measuring north-south locations on Earth is the equator, a great circle which is everywhere equidistant from the poles. Circles in planes parallel to the equator define north-south measurements called parallels, or lines of latitude (Figure 3). Latitude is expressed as an arc subtended between the equator and the parallel, as seen from the center of the Earth. Downtown Pasadena, California, is located at 34 degrees, 08 minutes, 44 seconds latitude north of the equator: 34° 08' 44" N.
One degree of latitude equals approximately 111 km on the Earth's surface, and by definition exactly 60 nautical miles. Because meridians converge at the poles, the length of a degree of longitude varies from 111 km at the equator to 0 at the poles where longitude becomes a point.
Rotation and Revolution
"Rotation" refers to an object's spinning motion about its own axis. "Revolution" refers the object's orbital motion around another object. For example, Earth rotates on its own axis, producing the 24-hour day. Earth revolves about the Sun, producing the 365-day year. A satellite revolves around a planet.
Earth's Rotation
The Earth rotates on its axis relative to the sun every 24.0 hours mean solar time, with an inclination of 23.45 degrees from the plane of its orbit around the sun. Mean solar time represents an average of the variations caused by Earth's non-circular orbit. Its rotation relative to "fixed" stars (sidereal time) is 3 minutes 56.55 seconds shorter than the mean solar day, the equivalent of one solar day per year.
Precession of Earth's Axis
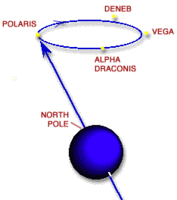Figure 4: Precession of Earth's Axis Over 26,000 Years (Source: NASA) Forces associated with the rotation of Earth cause the planet to be slightly oblate, displaying a bulge at the equator. The moon's gravity primarily, and to a lesser degree the sun's gravity, act on Earth's oblateness to move the axis perpendicular to the plane of Earth's orbit. However, due to gyroscopic action, Earth's poles do not "right themselves" to a position perpendicular to the orbital plane. Instead, they precess at 90 degrees to the force applied. This precession causes the axis of Earth to describe a circle having a 23.4 degree radius relative to a fixed point in space over about 26,000 years, a slow wobble reminiscent of the axis of a spinning top swinging around before it falls over.
Because of the precession of the poles over 26,000 years, all the stars, and other celestial objects, appear to shift west to east at the rate of .01 degree each year (360 degrees in 26,000 years). This apparent motion is the main reason for astronomers as well as spacecraft operators to refer to a common epoch such as J2000.0.
At the present time in Earth's 26,000 year precession cycle, a bright star happens to be very close, less than a degree, from the north celestial pole. This star is called Polaris, or the North Star.
Stars do have their own real motion, called proper motion. In our vicinity of the galaxy, only a few bright stars exhibit a large enough proper motion to measure over the course of a human lifetime, so their motion does not generally enter into spacecraft navigation. Because of their immense distance, stars can be treated as though they are references fixed in space. (Some stars at the center of our galaxy, though, display tremendous speeds as they orbit close to the massive black hole located there.)
Nutation
Superimposed on the 26,000-year precession is a small nodding motion with a period of 18.6 years and an amplitude of 9.2 arc seconds. This nutation can trace its cause to the 5 degree difference between the plane of the Moon's orbit, the plane of the Earth's orbit, and the gravitational tug on one other.
Revolution of Earth
Earth revolves in orbit around the sun in 365 days, 6 hours, 9 minutes with reference to the stars, at a speed ranging from 29.29 to 30.29 km/s. The 6 hours, 9 minutes adds up to about an extra day every fourth year, which is designated a leap year, with the extra day added as February 29th. Earth's orbit is elliptical and reaches its closest approach to the Sun, a perihelion of 147,090,000 km, on about January fourth of each year. Aphelion comes six months later at 152,100,000 km.
Epochs
Because we make observations from Earth, knowledge of Earth's natural motions is essential. As described above, our planet rotates on its axis daily and revolves around the sun annually. Its axis precesses and nutates. Even the "fixed" stars move about on their own. Considering all these motions, a useful coordinate system for locating stars, planets, and spacecraft must be pinned to a single snapshot in time. This snapshot is called an epoch.
By convention, the epoch in use today is called J2000.0, which refers to the mean equator and equinox of year 2000, nominally January 1st 12:00 hours Universal Time (UT). The "J" means Julian year, which is 365.25 days long. Only the 26,000-year precession part of the whole precession/nutation effect is considered, defining the mean equator and equinox for the epoch.
The last epoch in use previously was B1950.0 - the mean equator and equinox of 1949 December 31st 22:09 UT, the "B" meaning Besselian year, the fictitious solar year introduced by F. W. Bessell in the nineteenth century. Equations are published for interpreting data based on past and present epochs.
Making Sense
Given an understanding of the Earth's suite of motions – rotation on axis, precession, nutation, and revolution around the Sun – and given knowledge of an observer's location in longitude (Figure 1) and latitude (Figure 3), meaningful observations can be made. For example, to measure the precise speed of a spacecraft flying to Saturn, you have to know exactly where you are on the Earth's surface as you make the measurement, and then subtract out the Earth's motions from that measurement to obtain the spacecraft's speed. The same applies if you are trying to measure the proper motion of a distant star – or a star's subtle wobble, to reveal a family of planets.
The Celestial Sphere
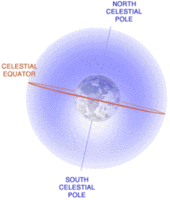Figure 5: The Celestial Sphere (Source: NASA) A useful construct for describing locations of objects in the sky is the celestial sphere, which is considered to have an infinite radius. The center of the Earth is the center of the celestial sphere, and the sphere's pole and equatorial plane are coincident with those of the Earth (see Figure 5). We can specify precise location of objects on the celestial sphere by giving the celestial equivalent of their latitudes and longitudes.
The point on the celestial sphere directly overhead for an observer is the zenith. An imaginary arc passing through the celestial poles and through the zenith is called the observer's meridian. The nadir is the direction opposite the zenith: for example, straight down from a spacecraft to the center of the planet.
Declination and Right Ascension
Figure 6: The Ecliptic Plane (Source: NASA) Declination (DEC) is the celestial sphere's equivalent of latitude and it is expressed in degrees, as is latitude. For DEC, + and - refer to north and south, respectively. The celestial equator is 0° DEC, and the poles are +90° and -90°.
Right ascension (RA) is the celestial equivalent of longitude. RA can be expressed in degrees, but it is more common to specify it in hours, minutes, and seconds of time: the sky appears to turn 360° in 24 hours, or 15° in one hour. So an hour of RA equals 15° of sky rotation.
Another important feature intersecting the celestial sphere (Figure 5) is the ecliptic plane (Figure 6). This is the plane in which the Earth orbits the Sun, 23.4° from the celestial equator. The great circle marking the intersection of the ecliptic plane on the celestial sphere is where the Sun and planets appear to travel, and where the Sun and Moon converge during their eclipses (hence the name).
The zero point for RA is one of the points where the ecliptic circle intersects the celestial equator circle. It is defined as the point where the Sun crosses into the northern hemisphere beginning spring: the vernal equinox, also known as the first point of Aries.
The RA and DEC of an object specify its position uniquely on the celestial sphere just as the latitude and longitude do for an object on the Earth's surface. For example, the very bright star Sirius has celestial coordinates 6 hr 45 min RA and -16° 43' DEC.
The equinoxes are times at which the center of the Sun is directly above the equator, marking the beginning of spring and autumn. The day and night would be of equal length at that time, if the Sun were a point and not a disc, and if there were no atmospheric refraction. Given the apparent disc of the Sun, and the refraction, day and night actually become equal at a point within a few days of each equinox.
| Disclaimer: This article is taken wholly from, or contains information that was originally published by, the NASA. Topic editors and authors for the Encyclopedia of Earth may have edited its content or added new information. The use of information from the NASA should not be construed as support for or endorsement by that organization for any new information added by EoE personnel, or for any editing of the original content. |
