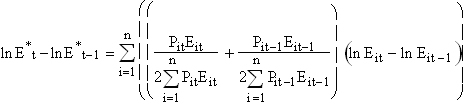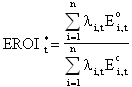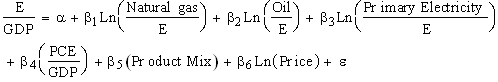Energy quality
Contents
- 1 Introduction One aspect of energy quality: a comparison of the energy content per unit mass and per unit volume for various sources. Energy quality refers to differences in the ability of a unit of energy (Energy quality) to produce goods and services for people. The usefulness of an energy system is determined by a complex combination of physical, technical, economic, and social attributes. These include gravimetric and volumetric energy density, power density, emissions, cost and efficiency of conversion, financial risk, amenability to storage, risk to human health, and ease of transport. No single metric of an energy system captures all such attributes. It stands to reason, therefore, that a comprehensive and balanced comparison of energy technologies should employ a range of metrics, with their strengths and weaknesses duly noted.
- 2 Aggregation by Heat Content
- 3 Economic Approaches to Energy Quality
- 4 Alternative Approaches to Energy Aggregation
- 5 Exergy
- 6 Case Study 1: Net Energy from Fossil Fuel Extraction in the US
- 7 Case Study 2: Causality in the Energy/GDP Relationship
- 8 Case Study 3: The Determinants of the Energy/GDP Relationship
- 9 Conclusions and Implications Application of the Divisia Index to energy (Energy quality) use in the U.S. economy illustrates the importance of energy quality in aggregate analysis. The quality-corrected index for EROI indicates that the energy surplus delivered by petroleum extraction in the US is smaller than indicated by unadjusted EROI. The trend over time in a quality-adjusted index of total primary energy use in the US economy is significantly different than and drops faster than the standard heat-equivalent index. Analysis of Granger causality and cointegration indicate a causal relationship running from quality-adjusted energy to GDP, but not from the unadjusted energy index. The econometric analysis of the energy/real GDP ratio indicates that the decline in industrial economies has been driven in part by the shift from coal to oil, gas, and primary electricity. Together these results suggest that accounting for energy quality reveals a relatively strong relationship between energy use and economic output. This runs counter to much of the conventional wisdom that technical improvements and structural change have decoupled energy use from economic performance. To a large degree, technical change and substitution has increased the use of higher quality energy and reduced use of lower quality energy. In economic terms this means that technical change has been "embodied" in the fuels and their associated energy converters. These changes have increased energy efficiency in energy extraction processes, allowed an apparent "decoupling" between energy use and economic output, and increased energy efficiency in the production of output.
Introduction One aspect of energy quality: a comparison of the energy content per unit mass and per unit volume for various sources. Energy quality refers to differences in the ability of a unit of energy (Energy quality) to produce goods and services for people. The usefulness of an energy system is determined by a complex combination of physical, technical, economic, and social attributes. These include gravimetric and volumetric energy density, power density, emissions, cost and efficiency of conversion, financial risk, amenability to storage, risk to human health, and ease of transport. No single metric of an energy system captures all such attributes. It stands to reason, therefore, that a comprehensive and balanced comparison of energy technologies should employ a range of metrics, with their strengths and weaknesses duly noted.
Aggregation by Heat Content
The most common way to measure energy is by heat content because all forms of energy can be completely converted to heat (Btus, joules, calories, kilowatt-hours). The aggregation of different energy types is accomplished by multiplying their mass or volume used times their heat content per unit mass or volume (see Table 1), and then summing them. Equation (2) illustrates this approach:
- <math>E_t = sum_{i=1}^N E_{it}</math> -- (2) </dd>
where E represents the enthalpy or thermal equivalent of fuel i (N types) at time t. For example, one gallon of motor gasoline contains 130.8 million joules and one cubic feet of natural gas contains 1.1 million joules. Thus one could add add the two types and quantities together and represent them as 131.9 joules. The world uses about 475x1018 joules energy each year. That quantity is the aggregation of dozens of different energy types added together by the "themal equivalent approach."
The advantage of the thermal equivalent approach is that it uses a simple and well-defined accounting system based on the conservation of energy, and the fact that thermal equivalents are easily and uncontroversially measured. This approach underlies most methods of energy aggregation in economics and ecology, such as trophic dynamics, national energy accounting, energy input-output modeling in economies and ecosystems, most analyses of the energy/GDP relationship, and energy efficiency, and most net energy analyses.
Despite its widespread use, aggregating different energy types by their heat units embodies a serious flaw: it implicitly assumes that "all joules are equal," i.e., that people value a heat unit of electricity the same as a heat unit of coal. Of course, this is not the case. Electricity performs important tasks that coal cannot, or it performs them more effectively. People are willing to pay 15 times more for a heat unit of electricity (in the U.S.) because of these differences. If all joules were equal, we wouldn't generate electricity from gas or coal in the first place given that two-thirds of the joules in the fuel input are lost as waste heat.
Taking energy quality into account in energy aggregation requires more advanced forms of aggregation. Some of these forms are based on concepts developed in the energy analysis literature such as exergy or emergy analysis. These methods take the following form:
- <math>E_t^* = sum_{i=1}^N lambda_{it} E_{it}</math> -- (3) </dd>
where the ?’s are quality factors that may vary among fuels and over time for individual fuels.
Economic Approaches to Energy Quality
From an economic perspective, the value of a heat equivalent of fuel is determined by its price. Price-taking consumers and producers set marginal utilities and products of the different forms of energy equal to their market prices. These prices and their marginal productivities and utilities are set simultaneously in general equilibrium. The value marginal product of a fuel in production is the marginal increase in the quantity of a good or service produced by the use of one additional heat unit of fuel multiplied by the price of that good or service. We can also think of the value of the marginal product of a fuel in household production.
The marginal product of a fuel is determined in part by a complex set of attributes unique to each fuel such as physical scarcity, capacity to do useful work, energy density, cleanliness, amenability to storage, safety, flexibility of use, cost of conversion, and so on. But the marginal product is not uniquely fixed by these attributes. Rather, the energy vector’s marginal product varies according to the activities in which it is used, how much and what form of capital, labor, and materials it is used in conjunction with, and how much energy is used in each application. As the price rises due to changes on the supply-side, users can reduce their use of that form of energy in each activity, increase the amount and sophistication of capital or labor used in conjunction with the fuel, or stop using that form of energy for lower value activities. All these actions raise the marginal productivity of the fuel. When capital stocks have to be adjusted, this response may be somewhat sluggish and lead to lags between price changes and changes in the value marginal product.
The heat equivalent of a fuel is just one of the attributes of the fuel and ignores the context in which the fuel is used, and thus cannot explain, for example, why a thermal equivalent of oil is more useful in many tasks than is a heat equivalent of coal. In addition to attributes of the fuel, marginal product also depends on the state of technology, the level of other inputs, and other factors. According to neoclassical theory, the price per heat equivalent of fuel should equal its value marginal product, and, therefore, represent its economic usefulness. In theory, the market price of a fuel reflects the myriad factors that determine the economic usefulness of a fuel from the perspective of the end-user.
Consistent with this perspective, the price per heat equivalent of fuel varies substantially among fuel types (see Table 1). The different prices demonstrate that end-users are concerned with attributes other than heat content. As Ernst Berndt observed, because of the variation in attributes among energy types, the various fuels and electricity are less than perfectly substitutable - either in production or consumption. For example, from the point of view of the end-user, a Btu of coal is not perfectly substitutable with a Btu of electricity; since the electricity is cleaner, lighter, and of higher quality, most end-users are willing to pay a premium price per Btu of electricity. However, coal and electricity are substitutable to a limited extent, since if the premium price for electricity were too high, a substantial number of industrial users might switch to coal. Alternatively, if only heat content mattered and if all energy types were then perfectly substitutable, the market would tend to price all energy types at the same price per Btu.
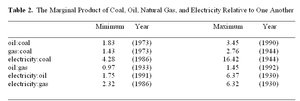
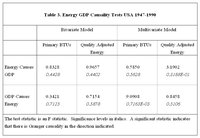
Do market signals (i.e. prices) accurately reflect the marginal product of inputs? Robert Kaufmann (1994) investigates this question in an empirical analysis of the relation between relative marginal product and price in US energy markets. To do so, he estimates a reduced form of a production function that represents how the fraction of total energy use from coal, oil, natural gas, and primary electricity (electricity from hydro and nuclear sources) affects the quantity of energy required to produce a given level of output (see Case Study 3, below). The partial derivatives of the production function with respect to each of the fuels gives the marginal product of individual fuels, in which marginal product is defined as the change in economic output given a change in the use of a heat unit of an individual fuel. The equations are used to calculate the marginal product for each fuel type for each year between 1955 and 1992. The time series for marginal products are compared among fuels, and these ratios are related to relative prices using a partial adjustment model. The results indicate that there is a long run relation between relative marginal product and relative price, and that several years of adjustment are needed to bring this relation into equilibrium. The results are summarized in Table 2, and suggest that over time, prices do reflect the marginal product - and hence the economic usefulness - of fuels.
Other analysts calculate the average product of fuels, which is a close proxy for marginal products. Adams and Miovic (1968) estimate a pooled annual cross-sectional regression model of industrial output as a function of fuel use in seven European economies from 1950 to 1962. Their results indicate that petroleum is 1.6 to 2.7 times more productive than coal in producing industrial output. Electricity is 2.7 to 14.3 times more productive than coal. Using a regression model of the energy/GDP ratio in the U.S., Cutler J. Cleveland et al. (1984) find that the quality factors of petroleum and electricity relative to coal were 1.9 and 18.3, respectively.
Price-Based Aggregation
If marginal product is related to its price, energy quality can be measured by using the price of fuels to weight their heat equivalents. The simplest approach defines the weighting factor (?’s) in Equation (3) as:
(5)
where Pit is the price per Btu of fuel. In this case, the price of each fuel is measured relative to the price of fuel type 1. Turvey and Nobay (1965) use Equation (4) to aggregate fuel use in the UK.
The quality index in Equation (5) embodies a restrictive assumption – that fuels are perfect substitutes – and the index is sensitive to the choice of numeraire. Because fuels are not perfect substitutes, a rise in the price of one fuel relative to the price of output will not be matched by equal changes in the prices of the other fuels relative to the price of output. For example, the rise in oil prices in 1979-80 would cause an aggregate energy index which uses oil as the numeraire to fall dramatically. An index that uses coal as the numeraire would show a large fall in 1968-74, one not indicated by the oil-based index.
To avoid dependence on a numeraire, Berndt (1978, 1990) proposed a discrete approximation to the Divisia index to aggregate energy. The formula for constructing the discrete Divisia index E* is:
(6)
where P are the prices of the n fuels, and E are the quantities of BTU for each fuel in final energy use. Note that prices enter the Divisia index via cost or expenditure shares. The Divisia index permits variable substitution among material types without imposing a priori restrictions on the degree of substitution. Diewert (1976) shows that this index is an exact index number representation of the linear homogeneous translog production function where fuels are homothetically weakly separable as a group from the other factors of production. With reference to Equation (4), f() = g() = ?ln(), while ?it is given by the average cost share over the two periods of the differencing operation.
Discussion
Aggregation using price has its shortcomings. Lau (1982) suggests that prices provide a reasonable method of aggregation if the aggregate cost function is homothetically separable in the raw material input prices. This means that the elasticity of substitution between different fuels is not a function of the quantities of non-fuel inputs used. This may be an unrealistic assumption in some cases. Also, the Divisia index assumes that the substitution possibilities among all fuel types and output are equal.
Another limit on the use of prices is that they generally do not exist for wastes. Thus, an economic index of waste flows is impossible to construct.
It is well-known that energy prices do not reflect their full social cost due to a number of market imperfections. This is particularly true for the environmental impact caused by their extraction and use. These problems lead some to doubt the usefulness of price as the basis for any indicator of sustainability. But with or without externalities, prices should reflect productivities. Internalizing externalities will shift energy use, which, in turn, will then change marginal products.
Moreover, prices produce a ranking of fuels (see Table 1) that is consistent with our intuition and with previous empirical research. One can conclude that government policy, regulations, cartels and externalities explain some of the price differentials among fuels, but certainly not the substantial ranges that exist. More fundamentally, price differentials are explained by differences in attributes such as physical scarcity, capacity to do useful work, energy density, cleanliness, amenability to storage, safety, flexibility of use, cost of conversion, and so on. Wipe away the market imperfections and the price per BTU of different energies would vary due to the different combinations of attributes that determine their economic usefulness. The different prices per BTU indicate that users are interested in attributes other than heat content.
Alternative Approaches to Energy Aggregation
While we argue that the more advanced economic indexing methods, such as Divisia aggregation, are the most appropriate way to aggregate energy use for investigating its role in the economy, the ecological economics literature proposes other methods of aggregation. We briefly review two of these methods in this section and assess limits on their ability to aggregate energy use.
Exergy
Ayres et al. (1996) and Ayres and Martiñas (1995) propose a system of aggregating energy and materials based on exergy. Exergy measures the useful work obtainable from an energy source or material, and is based on the chemical energy embodied in the material or energy based on its physical organization relative to a reference state. Thus, exergy measures the degree to which a material is organized relative a random assemblage of material found at an average concentration in the crust, ocean or atmosphere. The higher the degree of concentration, the higher the exergy content. The physical units for exergy are the same as for energy or heat, namely kilocalories, joules, BTUs, etc. For fossil fuels, exergy is nearly equivalent to the standard heat of combustion; for other materials specific calculations are needed that depend on the details of the assumed conversion process.
Ayres argues that exergy has a number of useful attributes for aggregating heterogeneous energy and materials. Exergy is a property of all energy and materials and in principle can be calculated from information in handbooks of chemistry and physics (e.g., Linde 1991-1992) and secondary studies (e.g., Szargut et al. 1988). Thus, exergy can be used to measure and aggregate natural resource inputs as well as wastes. For these reasons, Ayres argues that exergy forms the basis for a comprehensive resource accounting framework that could "provide policy-makers with a valuable set of indicators." One such indicator is a general measure of "technical efficiency," the efficiency with which "raw" exergy from animals or inanimate source is converted into final services. A low exergy efficiency implies potential for efficiency gains for converting energy and materials into goods and services. Similarly, the ratio of exergy embodied in material wastes to exergy embodied in resource inputs is the "most general measure of pollution". Ayres and Martiñas (1995) also argue that the exergy of waste streams is a proxy for their potential ecotoxicity or harm to the environment, at least in general terms.
From an accounting perspective, exergy is appealing because it is based on the science and laws of thermodynamics and thus has a well-established system of concepts, rules, and information that are available widely. But like enthalpy, exergy should not be used to aggregate energy and material inputs aggregation because it is one-dimensional. Like enthalpy, exergy does not vary with, and hence does not necessarily reflect attributes of fuels that determine their economic usefulness, such as energy density, cleanliness, cost of conversion, and so on. The same is true for materials. Exergy cannot explain, for example, impact resistance, heat resistance, corrosion resistance, stiffness, space maintenance, conductivity, strength, ductility, or other properties of metals that determine their usefulness. Like prices, exergy does not reflect all the environmental costs of fuel use. The exergy of coal, for example, does not reflect coal’s contribution to global warming or its impact on human health relative to say natural gas. As Ayres (1997) himself notes, the exergy of wastes is at best a rough first-order approximation of environmental impact because it does not vary with the specific attributes of a waste material and its receiving environment that cause harm to organisms or that disrupt biogeochemical cycles. In theory exergy can be calculated for any energy or material, but in practice, the task of assessing the hundreds (thousands?) of primary and intermediate energy and material flows in an economy is daunting.
Emergy
Odum (1996) analyzes energy and materials with a system that traces their flows within and between society and the environment. It is important to differentiate between two aspects of Odum’s contribution. The first is his development of a biophysically-based, systems-oriented model of the relationship between society and the environment. Here Odum’s early contributions helped lay the foundation for the biophysical analysis of energy and material flows, an area of research that forms part of the intellectual backbone of ecological economics. The insight from this part of Odum’s work is illustrated by the fact that ideas he emphasized—energy and material flows, feedbacks, hierarchies, thresholds, time lags—are key concepts of the analysis of sustainability in a variety of disciplines.
The second aspect of Odum’s work, which we are concerned with here, is a specific empirical issue: the identification, measurement, and aggregation of energy and material inputs to the economy, and their use in the construction of indicators of sustainability. Odum measures, values, and aggregates energy of different types by their transformities. Transformities are calculated as the amount of one type of energy required to produce a heat equivalent of another type of energy. To account for the difference in quality of thermal equivalents among different energies, all energy costs are measured in solar emjoules (sej), the quantity of solar energy used to produce another type of energy. Fuels and materials with higher transformities require larger amounts of sunlight to produce and therefore are considered more economically useful.
Several aspects of the emergy methodology reduce its usefulness as a method for aggregating energy and/or material flows. First, like enthalpy and exergy, emergy is one-dimensional because energy sources are evaluated based on the quantity of embodied solar energy and crustal heat. But is the usefulness of a fuel as an input to production related to its transformity? Probably not. Users value coal based on it heat content, sulfur content, cost of transportation and other factors that form the complex set of attributes that determine its usefulness relative to other fuels. It is hard to imagine how this set of attributes is in general related to—much less determined by—the amount of solar energy required to produce coal. Second, the emergy methodology is inconsistent with its own basic tenant, namely that quality varies with embodied energy or emergy. Coal deposits that we currently extract were laid down over many geological periods that span half a billion years. Coals thus have vastly different embodied emergy, but only a single transformity for coal is normally used. Third, the emergy methodology depends on plausible but arbitrary choice of conversion technologies (e.g., boiler efficiencies) that assume users choose one fuel relative to another and other fuels based principally on their relative conversion efficiencies in a particular application. Finally, the emergy methodology relies on long series of calculations with data that vary in quality. Yet little attention is paid to the sensitivity of the results to data quality and uncertainty, leaving the reader with little no sense of how precise or reliable the emergy calculations are.
It is instructive to compare emergy analysis with other popular methods of energy and material flow accounting, such as input-output analysis. In emergy analysis, unlike input-output analysis, each process in the system is assigned the total value of the total emergy input to the Earth because according to Odum, “each process is considered to be a co-product of the global geological cycle and cannot be produced independently with less than the total emergy.” This creates an accounting system that does not conform to the principle that the total value of all inputs to each process equal the total value of all outputs from that process. Input-output methods do conform to this principle. Because of this, emergy techniques have been characterized as simplistic, contradictory, misleading and inaccurate. Rebuttals to these critiques have also been published, but the persistent skepticism seems to stem from the difficulty in obtaining detail about the underlying computations, and a lack of formal links with related concepts in other disciplines, like the input-output method.
Case Study 1: Net Energy from Fossil Fuel Extraction in the US
One technique for evaluating the productivity of energy systems is net energy analysis, which compares the quantity of energy delivered to society by an energy system to the energy used directly and indirectly in the delivery process. Cottrell (1955) and Odum were the first to identify the economic importance of net energy. Energy return on investment (EROI) is the ratio of energy delivered to energy costs. There is a long debate about the relative strengths and weaknesses of net energy analysis. One restriction on net energy analysis’ ability to deliver the insights it promises is its treatment of energy quality. In most net energy analyses, inputs and outputs of different types of energy are aggregated by their thermal equivalents. Following, this case study illustrates how accounting for energy quality affects calculations for the EROI of the US petroleum sector from 1954-1992 from 1954-1992.
Methods and Data
Following the definitions in Equation (3), a quality-corrected EROI* is defined by:
(7)
where ?i, t is the quality factor for fuel type i at time t and Eo and Ec are the thermal equivalents of energy outputs and energy inputs, respectively. We construct divisia indices for energy inputs and outputs to account for energy quality in the numerator and denominator. The prices for energy outputs (oil, natural gas, natural gas liquids) and energy inputs (natural gas, gasoline, distillate fuels, coal, electricity) are the prices paid by industrial end-users for each energy type.
Cutler J. Cleveland (1992) provides full details on the data and methods presented here. Energy inputs include only industrial energies: the fossil fuel and electricity used directly and indirectly to extract petroleum. The costs include only those energies used to locate and extract oil and natural gas and prepare them for shipment from the wellhead. Transportation and refining costs are excluded from this analysis. Output in the petroleum industry is the sum of the marketed production of crude oil, natural gas, and natural gas liquids.
The direct energy cost of petroleum is the fuel and electricity used in oil and gas fields (Bureau of Census, various years). Indirect energy costs include the energy used to produce material inputs and to produce and maintain the capital used to extract petroleum. The indirect energy cost of materials and capital is calculated from data for the dollar cost of those inputs to petroleum extraction processes. Energy cost of capital and materials is defined as the dollar cost of capital depreciation and materials times the energy intensity of capital and materials (BTU/$). The energy intensity of capital and materials is measured by the quantity of energy used to produce a dollar’s worth of output in the industrial sector of the U.S. economy. That quantity is the ratio of fossil fuel and electricity use to real GDP produced by industry.
Results and Conclusions
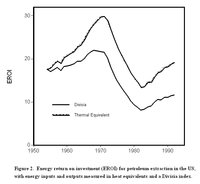
The thermal equivalent and Divisia EROI for petroleum extraction show significant differences (see Figure 2). The quality-corrected EROI declines faster than the thermal-equivalent EROI. The thermal-equivalent EROI increases by 60 percent relative to the Divisia EROI between 1954 and 1992. This difference is driven largely by changes in the mix of fuel qualities in energy inputs. Electricity, the highest quality fuel, is an energy input but not an energy output. Its share of total energy use rises from 2 to 12 percent over the period; its cost share increases from 20 to 30 percent. Thus, in absolute terms, the denominator in the Divisia EROI is weighted more heavily than in the thermal equivalent EROI. The Divisia-weighted quantity of refined oil products is larger than that for gas and coal. Thus, the two highest quality fuels, electricity and refined oil products, comprise a large and growing fraction of the denominator in the Divisia EROI compared to the thermal equivalent EROI. Thus the Divisia denominator increases faster than the heat-equivalent denominator causing EROI to decline faster in the former case.
Case Study 2: Causality in the Energy/GDP Relationship
One of the most important questions about the environment-economy relationship is the strength of the linkage between economic growth and energy use. With a few exceptions, most analyses ignore the effect of energy quality in the assessment of this relationship. One statistical approach to address this question is Granger causality and/or cointegration analysis. Granger causality tests whether (1) one variable in a relation can be meaningfully described as a dependent variable and the other variable an independent variable, (2) the relation is bi-directional, or (3) no meaningful relation exists at all. This is usually done by testing whether lagged values of one of the variables adds significant explanatory power to a model which already includes lagged values of the dependent variable and perhaps also lagged values of other variables.
While Granger causality can be applied to both stationary and integrated time series (time series which follow a random walk), cointegration applies only to linear models of integrated time series. The irregular trend in integrated series is known as a stochastic trend as opposed to a simple linear deterministic time trend. Time series of GDP and energy use usually are found to be integrated. Cointegration analysis aims to uncover causal relations among variables by determining if the stochastic trends in a group of variables are shared by the series so that the total number of unique trends is less than the number of variables. It can also be used to test if there are residual stochastic trends which are not shared by any other variables. This may be an indication that important variables have been omitted from the regression model or that the variable with the residual trend does not have long-run interactions with the other variables.
Either of these conclusions could be true should there be no cointegration. The presence of cointegration can also be interpreted as the presence of a long-run equilibrium relationship between the variables in question. The parameters of an estimated cointegrating relation are called the cointegrating vector. In multivariate models there may be more than one such cointegrating vector.
Granger Causality and the Energy GDP Relation
A series of analysts use statistical tests developed by Granger (1969) or Sims (1972) to evaluate whether energy use or energy prices determine economic growth, or whether the level of output in the US and other economics determine energy use or energy prices. Generally, the results are inconclusive. Where significant results are obtained, they indicate causality running from output to energy use.
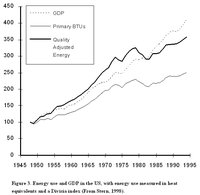
Stern (1993) tests US data (1947-1990) for Granger causality in a multivariate setting using a vector autoregression (VAR) model of GDP, energy use, capital, and labor inputs. He measures energy use by its as thermal equivalents and the Divisia aggregation method discussed above. The relation among GDP, the thermal equivalent of energy use, and the Divisia energy use indicates that there is less ’decoupling’ between GDP and energy use when the aggregate measure for energy use accounts for qualitative differences (see Figure 3). The multivariate methodology is important because changes in energy use frequently are countered by substitution with labor and/or capital and thereby mitigate the effect of changes in energy use on output. Weighting energy use for changes in the composition of the energy input is important because a large part of the growth effects of energy are due to substitution of higher quality energy sources such as electricity for lower quality energy sources such as coal (see Figure 1).
Bivariate tests of Granger causality show no causal order in the relation between energy and GDP in either direction regardless of the measure used to qualify energy use (see Table 3). In the multivariate model with energy measured in primary BTUs, GDP was found to ’Granger cause’ energy use. However, when both innovations - a multivariate model and energy use is adjusted for quality - are employed, energy ’Granger causes’ GDP. These results show that adjusting energy for quality is important as is considering the context within which energy use is occurring. The result that energy use plays an important role in determining the level of economic activity is consistent with the price-based studies of Hamilton (1983) and Burbridge and Harrison (1984).
Cointegration and the Energy GDP Relation
Stern (1998) tests for cointegration between energy use and economic activity in the same multivariate model used in Stern (1993) with US data from 1948 to 1994. If a multivariate approach helps uncover the direction of Granger causality between energy and GDP, then a multivariate approach should clarify the cointegrating relations among variables. The Johansen methodology is used to test for the number of cointegrating vectors in the multivariate Vector Error Correction Model (VECM) estimate their parameters, and the rate at which energy use and economic activity adjusts to disequilibrium in the long-run relations. The VECM is given by:
(8)
in which y is a vector of variables (in logarithms), ? t is a vector of random disturbances, ? is the first difference operator, t is a deterministic time trend, y is a vector of coefficients to be estimated, ? is a matrix of adjustment coefficients (to be estimated), ? is the matrix of cointegrating vectors (to be estimated), and the ?i are matrices of short-run dynamics coefficients (to be estimated). The test for the number of cointegrating vectors determines the dimensions of ? and ?.
The cointegrating vectors indicate that energy use and GDP are present in both cointegrating relations but the elements of ? indicate that these cointegrating relations affect the equation for energy use only. This result indicates that there is a statistically significant relation between energy use and GDP, but the direction of causality run from economic activity to energy use. This result is consistent with Stern (1993).
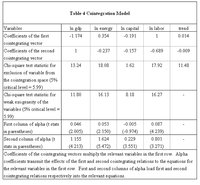
Table 4 presents the results for the model using the quality-adjusted energy index. The third row in Table 4 presents tests for excluding each of the variables from the long run relation. Restrictions that eliminate energy from the long-run relationships are rejected while the same restrictions for capital cannot be rejected. However, the statistics in the fourth row show that none of the variables can be treated as exogenous variables. The causal pattern is in general mutual. The fifth and sixth rows show the signs and significance of the adjustment coefficients. The first cointegrating relation has no significant effect on the capital equation. However, all the other coefficients are significant. This again confirms the mutual causality pattern.
Use of quality-adjusted energy indices clearly has an important effect on analyses of Granger causality and cointegration. When energy is measured in thermal equivalents, research predominantly finds that either there is no relation between energy and GDP or that the relation runs from GDP to energy in both bivariate and multivariate models. The implications for the importance of energy in the economy are quite different in the two cases.
Case Study 3: The Determinants of the Energy/GDP Relationship
One of the most widely cited macroeconomic indicators of sustainability is the ratio of total energy use to total economic activity, or the energy/real GDP ratio (E/GDP ratio). This ratio has declined since 1950 in many industrial nations. Controversy arises regarding the interpretation of this decline. Many economists and energy analysts argue that the declines indicate that the relation between energy use and economic activity is relatively weak. This interpretation is disputed by many biophysical economists. They argue that the decline in the E/GDP ratio overstate the ability to decouple energy use and economic activity because many analyses of the E/GDP ratio ignore the effect of changes in energy quality (see Figure 1).
The effect of changes in energy quality (and changes in energy prices, and types of goods and services produced and consumed) on the E/GDP ratio can be estimated using Equation (9), which was developed by Gever et al., (1986) and Cleveland et al., (1984):
(9)
in which E is the total primary energy consumption (measured in heat units), GDP is real GDP, primary electricity is electricity generated from hydro, nuclear, solar, or geothermal sources, PCE is real personal consumption expenditures spent directly on energy by households, Product Mix measures the fraction of GDP that originates in energy intensive sectors (e.g., chemicals) or non-energy intensive sectors (e.g., services), and Price is a measure of real energy prices.
The effect of energy quality on the E/GDP ratio is measured by the fraction of total energy consumption from individual fuels. The sign on the regression coefficients ?1, ?2, and ?3 is expected to be negative because natural gas, oil, and primary electricity can do more useful work (and therefore generate more economic output) per heat unit than coal. The rate at which an increase in the use of natural gas, oil, or primary electricity reduces the E/GDP ratio is not constant. Engineering studies indicate that the efficiency with which energies of different types are converted to useful work depends on their use. Petroleum can provide more motive power per heat unit of coal, but this advantage nearly disappears if petroleum is used as a source of heat (Adams and Miovic, 1968). From an economic perspective, the law of diminishing returns implies that the first uses of high quality energies are directed at tasks that are best able to make use of the physical, technical, and economic aspects of an energy type that combine to determine its high quality status. As the use of a high quality energy source expands, it is used for tasks that are less able to make use of the attributes that confer high quality. The combination of physical differences in the use of energy and the economic ordering in which they are applied to these tasks implies that the amount of economic activity generated per heat unit diminishes as the use of a high quality energy expands. Diminishing returns on energy quality is imposed on the model by specifying the fraction of the energy budget from petroleum, primary electricity, natural gas, or oil in natural logarithms. This specification ensures that the first uses of high quality energies decreases the energy/GDP ratio faster than the last uses.
The regression results indicate that Equation (9) can be used to account for most of the variation in the energy/GDP ratio for France, Germany, Japan, and the United Kingdom during the post-war period and in the US since 1929. All of the variables have the sign as expected by economic theory, are statistically significant, and the error terms have the properties assumed by the estimation technique.
Analysis of regression results indicate that changes in energy mix can account for a significant portion of the downward trend in E/GDP ratios. The change from coal to petroleum and petroleum to primary electricity is associated with a general decline in the E/GDP ratio in France, Germany, the United Kingdom, and the US during the post-war period (Figure 4a-d). The fraction of total energy consumption that is supplied by petroleum increases steadily in each nation through the early 1970s. After the first oil shock, the fraction of total energy use from petroleum is steady or declines slightly in these four nations. However, energy mix continues to reduce the energy/real GDP ratio after the first oil shock because the fraction of total energy use from primary electricity rises steadily. The effect of changes in energy mix on the E/GDP ratio shows no trend over time in Japan, where the fraction of total energy consumption that is supplied by primary electricity falls through the early 1970s and increases steadily thereafter. This U shape offsets the steady increase in the fraction of total energy use from petroleum that occurs prior to 1973.
These regression results indicate that the historical reduction in the E/GDP ratio is associated with shifts in the types of energies used and the types of goods and services consumed and produced. Diminishing returns to high quality energies and the continued consumption of good from energy-intensive sectors such as manufacturing imply that the ability for changes in the composition of inputs and outputs to reduce the energy/real GDP ratio further are limited.
Conclusions and Implications Application of the Divisia Index to energy (Energy quality) use in the U.S. economy illustrates the importance of energy quality in aggregate analysis. The quality-corrected index for EROI indicates that the energy surplus delivered by petroleum extraction in the US is smaller than indicated by unadjusted EROI. The trend over time in a quality-adjusted index of total primary energy use in the US economy is significantly different than and drops faster than the standard heat-equivalent index. Analysis of Granger causality and cointegration indicate a causal relationship running from quality-adjusted energy to GDP, but not from the unadjusted energy index. The econometric analysis of the energy/real GDP ratio indicates that the decline in industrial economies has been driven in part by the shift from coal to oil, gas, and primary electricity. Together these results suggest that accounting for energy quality reveals a relatively strong relationship between energy use and economic output. This runs counter to much of the conventional wisdom that technical improvements and structural change have decoupled energy use from economic performance. To a large degree, technical change and substitution has increased the use of higher quality energy and reduced use of lower quality energy. In economic terms this means that technical change has been "embodied" in the fuels and their associated energy converters. These changes have increased energy efficiency in energy extraction processes, allowed an apparent "decoupling" between energy use and economic output, and increased energy efficiency in the production of output.
The manner in which these improvements have been largely achieved should give pause for thought. If decoupling is largely illusory, any rise in the cost of producing high quality energy vectors could have important economic impacts. Such an increase might occur if use of low cost coal to generate electricity is restricted on environmental, in particular climate change, grounds. If the substitution process cannot continue, further reductions in the E/GDP ratio would slow. Three factors might limit future substitution to higher quality energy. First, there are limits to the substitution process. Eventually all energy used would be of the highest quality variety - electricity - and no further substitution could occur. Future discovery of a yet higher quality energy source might mitigate this but it would be unwise to rely on the discovery of new physical principles. Second, as different energy sources are not perfect substitutes, the substitution process could have economic limits that will prevent full substitution. For example, it is difficult to imagine an airliner running on electricity. Third, it is likely that supplies of petroleum - which is of higher quality than coal - will begin to decline fairly early in the next century.
Finally, our conclusions do not imply that one-dimensional and/or physical indicators are universally inferior to the economic indexing approach we endorse. As one reviewer noted, ecologists might raise the problem of Leibig’s law of the minimum in which the growth or sustainability of a system is constrained by that single critical element in least supply. Exergy or mass are appropriate if the object of analysis is a single energy or material flux. Physical units are also necessary to valuate those flows. Integrated assessment of a material cycle within and between the environment and the economy is logical based on physical stocks and flows. However, when the question being asked requires the aggregation of energy flows in economic system, an economic approach such as Divisa aggregation or a direct measure of marginal product embody a more tenable set of assumptions than does aggregation by one dimensional approaches.