Predator-prey cycles

Predator-prey cycles are characterized by regularly spaced increases and decreases in the population sizes or densities of a predator and its prey. Classically, the predator is a carnivorous species and the prey is an herbivorous species. However, carnivores that prey on other carnivores, herbivores feeding on plants, and even parasites attacking their host organisms are sometimes considered to have the same relationship, and so to be predator-prey systems. The predator population’s fluctuations follow those of the prey population through time. That is, the prey population begins to increase while the predator population is still decreasing and the prey population decreases while the predator population is still increasing. The classic (and simplest) explanation of these cycles is that the predator drives the changes in the prey population (by catching and killing its members) and the prey (as the predator’s food supply) drives the predator’s population changes, but a lag between the population responses of predator and prey cause the two cycles to be out of phase with one another. However, this explanation has been challenged, and it may not be the only viable explanation for the pattern.
In general, the increases and declines of population density and the regulation of those changes are important aspects of community organization with the potential for practical applications such as pest control and conservation of endangered species (IUCN Red List Criteria for Endangered). Population cycles, in which the population increases and decreases repeatedly, at more or less regular intervals, have been at the center of the attempt to understand population fluctuations. Cycles are useful because the changes can be anticipated with some confidence and more changes may occur in a given time period than in an irregularly fluctuating population. The regulation of predator-prey cycles has been an important part of these studies, and it was the focus of a pioneering attempt at mathematical modeling in ecology. Alfred Lotka and Vito Volterra developed the classical mathematical model independently and a simplified, intuitive development of their model is a good place to start consideration of predator-prey cycles.
Contents
- 1 The Logistic Model for Population Growth
- 2 The Logistic Equation Refined for Prey Population Growth
- 3 The Logistic Equation Perturbed for Predator Population Growth
- 4 Graphic Representations of Population Growth
- 5 The Graph for the Prey Population
- 6 The Graph for the Predator Population
- 7 The Graphical Solution Involving Both Predator and Prey
- 8 The Model and Predator-Prey Systems in Nature
- 9 Further Reading
The Logistic Model for Population Growth
The Lotka-Volterra predator-prey model is based on the logistic model for population growth (dN/dt = rN((K – N)/K)), in which dN/dt is the change in population size or density (N) with time (t), the d’s in the numerator and denominator are symbols for change. On the right hand side of the equation, r is a measure of the population’s ability to grow under ideal conditions and is often called the intrinsic rate of increase, K is the number of individuals or density of the population that can be continually supported by the environment (it is called the carrying capacity of the environment for the species), and ((K – N)/K) is the total of all environmental factors working against the growth of the population (it is the environmental resistance to population growth). The model’s equations do not look much like the logistic equation because of the assumptions that (1) the regulation of the prey population’s growth and size is entirely dependent on the predator catching, killing and eating members of the prey population, and (2) the regulation of the predator population’s growth and size is entirely dependent on the availability of prey to be caught, killed and eaten. All other aspects of environmental resistance are considered to be inconsequential. Considering the simplest system of one predator species and one prey species, the model consists of two equations, one for population growth in each species.
The Logistic Equation Refined for Prey Population Growth
The equation for the growth of the prey population under the assumption that it is entirely controlled by predation is—
In the equation dH/dt is the change in the prey population size or density with time. H is the prey population size (H for herbivore, the classical prey item) and t is time. Hence, dH/dt is the change in population size of the prey with a change in (or the passing of) time. On the right hand side of the equation, H is the population size or density of the prey, r is the intrinsic rate of increase of the prey population (its rate of increase in the absence of predators, in the presence of plenty of food, and all other requirements), P is the predator population size or density, and p is a factor which, in the simplified approach used here, measures the impact of a single predator individual on the population growth of the prey species or measures the intensity of the predator’s negative impact on the prey population’s growth.
The equation is intuitively logical in that: In the absence of predators (P = 0), pHP becomes zero and the prey population increases exponentially at a rate equal to rH. Under these conditions, of course, the prey population would soon encounter other aspects of environmental resistance to its growth, such as insufficient food, or attack by parasites and disease. In the presence of predators, the prey population will increase or decrease dependent upon the predator population size (P) and the intensity of the predator’s impact on the prey population (measured by p). But why is H included in the term for predator impact on prey? Intuitively, the more prey items available, the more the predators will be able to find, capture, kill and eat. In other words, predation in the model is a density dependent phenomenon which will be more intense at high density of prey. Note also that the generic environmental resistance term ((K – N)/K) of the logistic equation is replaced by the negatively signed term pHP. This replacement follows because the model assumes that predation keeps the prey population below the level at which other environmental resistance factors would come into play. That is, the model assumes that there is always enough food, space, nest sites and other prey necessities because the predator holds the prey population below the level that would bring those resources into short supply.
The Logistic Equation Perturbed for Predator Population Growth
The equation for the growth of the predator population under the assumption that it is entirely controlled by its food supply (the prey population) is—
Where dP/dt is the change in predator population size with time, P is the predator’s population size or density, H is still the prey population size or density, m is the mortality rate of the predator in the absence of prey, and h can be thought of as a measure of the impact of a single prey individual on the growth of the predator population or a measure of the usefulness of the prey to the predator.
The equation, as written above, shows the parallel logic with the prey population growth equation, but it is usually written, in a more mathematically sensible way, with the positive term first:
The equation is intuitively logical in that: In the absence of prey (H = 0), hHP = 0 and the predator population will decline exponentially (-mP). In the presence of prey, the predator population will change at a rate dependent upon the prey population size (H), its own population size (P) and the “usefulness” of the prey to the predator (measured by h). The environmental resistance term of the logistic equation ((K –N)/K) is replaced by the availability or shortage of prey.
Graphic Representations of Population Growth
The equations can be solved graphically with the prey population size or density graphed on the X (horizontal) axis and the predator population size or density graphed along the Y (vertical) axis. To explore the interpretation of these graphs consider the graphs for the predator and prey populations separately followed by the model’s solution with both on the same axes.
The Graph for the Prey Population
First consider the prey population’s graph. The model assumes that the prey population’s growth depends only on the predator’s population, so the equation for prey population growth is used to determine the predator population size that reduces dH/dt to 0. Solving the equation for dH/dt = 0, based on predator population size or density gives:
Note that the prey’s zero growth line is determined by the ratio of prey [[population growth] rate] (r) and the predator population’s impact on prey population growth (p), two factors that would intuitively be involved in controlling the growth of the prey population.
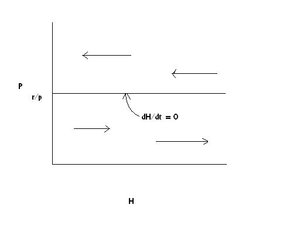
Figure 1 illustrates the graph for the growth of the prey population under the assumptions of the model.
Below the zero growth line for the prey in Figure 1, along which the predator population size or density is equal to r/p, the prey population increases. Intuitively, this is because there are not enough predators to catch, kill and eat prey faster than the prey can give birth to new individuals. This is shown by the right-directed arrows on the graph. However, above the zero growth line, the predators are so numerous that they capture, kill and eat prey faster than the prey can reproduce, and the prey population declines, indicated by the left-directed arrows on the graph.
The Graph for the Predator Population
The solution for the predator population’s growth in response to the prey population size is shown in Figure 2, in which the same axes are used.
Because the model assumes that predator population size is regulated entirely by its food supply, i.e., the prey population size, there is again a single prey population (H = m/h) which results in a vertical zero growth line on the graph.
Note that the zero growth line is determined by a relationship between the mortality of predators in the absence of prey (m) and the positive impact of the prey on the predator (h). Intuition affirms that these factors would have an impact on predator population growth.
When the prey population size or density is above m/h (to the right of m/h on Figure 2), the predator has enough food available to support an increase in its population. The upward directed arrows indicate this growth. If the prey population falls below m/h (to the left of m/h on the graph), the predator population suffers from inability to find enough food and declines as shown by the downward directed arrows.
The Graphical Solution Involving Both Predator and Prey
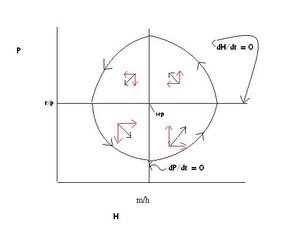
The interesting solution occurs when both populations are graphed on the same axes as in Figure 3.
The graph of Figure 3 is divided into four quadrants by the two zero growth lines. The right and left directed red arrows indicate the direction of growth (increase or decrease) of the prey population, and the up and down directed red arrows indicate the growth or decline of the predator population in each quadrant of the graph. The black arrow associated with each pair of red arrows indicates the summed growth and/or decline of both predator and prey in that quadrant.
The counterclockwise directed circle outlines the cyclic nature of the relationship: In the lower left hand quadrant, the predator population declines because there are too few prey available to sustain its growth; and the prey population increases because there are too few predators to stop its growth. This moves the populations into the lower right hand quadrant in which both increase. Note the increase in prey numbers precedes that of predator numbers. With both species increasing, the system moves into the upper right hand quadrant in which the prey begins to decrease under the increased predator population’s predatory activity. The predator continues to increase because there are still abundant prey present. These interactions drive the system into the upper left hand quadrant where both decline. Note again, the prey decline begins before the predator decline. With the decline of both, the system returns to the lower left hand quadrant and the cycle is complete and will be repeated according to the model.
The point where the two zero growth lines intersect is a stable equilibrium point (sep on Figure 3) around which the population sizes or densities fluctuate.
Another, perhaps more familiar, representation of the cycle is given by a graph of both populations’ growth and decline through time (Figure 4).
The graph in Figure 4 is directly derivable from the graph in Figure 3, so it is no surprise that the prey population leads the predator population through the cycle in this graph as well. That too makes intuitive sense. The predator cannot detect a decrease in prey immediately, but must experience the greater difficulty of finding prey and the starvation which results with the passage of time. That starvation and other forms of mortality, as well as difficulty producing young, all resulting from a declining food supply, make up the predator’s response. Nor can the prey respond immediately to the predator’s declining numbers. More prey are left alive because fewer predators are catching, killing and eating fewer of them, but to increase in numbers, the prey must reproduce, and that takes time so there is a lag in the response of each population to the changes that take place in the other. Increasing numbers of predator or prey result in delayed responses in the opposite population for similar reasons.
The Model and Predator-Prey Systems in Nature
Are such cyclic systems common in Nature? No. How well does the model predict population changes in the real world? Not well, and some of its shortcomings are apparent. The one-predator-one-prey system is highly oversimplified compared to the situation in a natural community. If more than one prey species were available, the predator could just switch to another prey species when one of its victims' populations declined to a size that made its members difficult for the predator to find. The predator population would not fluctuate as in the model unless all of its prey species declined and increased in synchrony. If more than one predatory species were involved, reality would be more complex than the model as well and populations would not follow the neat ups and downs of the model.
However, a few predator-prey systems in nature seem to follow the general pattern of the model quite well. An analysis of the annual harvest of Canada lynx and snowshoe hare pelts in the 1800’s and early 1900’s in North America produced one example. The hare is the primary prey of the lynx and the two populations’ fluctuations showed a pattern very similar to that predicted by the Lotka-Volterra model, producing a graph similar to Figure 4. The populations peaked about every ten years and they dropped to their low points about five years after each peak, also bottoming out approximately every ten years. As the model suggests, the lynx’s fluctuations followed the hare’s in time. Some studies of lemming and vole populations and their predators, foxes and owls, also show such a cycle with a period of approximately four years instead of ten.
These and most other systems that follow the Lotka-Volterra model reasonably well are found in arctic or sub-arctic latitudinal zones. Arctic communities have fewer species, than those in temperate and especially tropical zones, therefore single- predator-single-prey systems are more closely approximated in arctic systems than in more equatorial systems. Perhaps this is why the simple model closely approximates reality in those systems but does not work well in the more complex systems.
However, even in the arctic systems the cause and effect may not be consistent with the model. If the hare’s food supply, rather than lynx predation, were controlling the hare population, would not the same pattern result? Each population fluctuating in response to its food supply would result in the pattern of Figure 4, but the Lotka-Volterra model would not be the explanation for the pattern. There is some evidence that the hare’s food supply, or an interaction of predation with the hare’s food supply, is a better explanation for these cycles than the Lotka-Volterra model.
So, many predator-prey systems do not cycle as the model predicts and those that do may do so for reasons not predicted by the model. More elaborate predator-prey population models have been developed. Some of them incorporate additional factors such as those mentioned above. Such complex systems and analyses are beyond the reach not only of the Lotka-Voterra model but of many of the more elaborate models as well. Despite the fact that the Lotka-Volterra predation model is not complex enough to model the real world particularly well, it was an important early effort and the starting point for many of the more complex predator–prey models which more closely approach reality. The study of all these models has led to a more thorough understanding of ecological communities as well as of the regulation of predator-prey cycles.
Predation is recognized as one of the organizing forces in community ecology, though ecologists continue to explore its various implications. How frequently do predators regulate populations of their prey, in which taxonomic groups, in which ecological communities, and under what abiotic conditions? The answers to these questions have important application potential. While predators must often have an impact on the populations of their prey, so do a lot of other factors such as food supply, disease and competition. The roles of the various factors vary in different systems. As a result it is often difficult to separate the role of predators in population regulation from the roles of the other factors, and to determine whether predators can be effectively used in pest control or if control of their predator populations can protect endangered species (IUCN Red List Criteria for Endangered). The study of predator-prey cycles has and will continue to contribute to the solution of these and other problems.
Further Reading
- Colinvaux, Paul. 1978. Why Big Fierce Animals are Rare. Princeton, New Jersey: Princeton University Press. ISBN: 0691023646.
- Gabriel, Wilfried. "Predator-Prey Dynamics with Type-Two Functional Response" from The Wolfram Demonstrations Project. Contributed by: Wilfried Gabriel.
- Gotelli, Nicholas J. 2008. A Primer of Ecology. Sunderland, Massachusetts: Sinauer Associates, Inc. ISBN: 0878933182.
- Harms, William. Three Trophic-Level Ecosystem Simulator.
- Trophic Links: Predation and Parasitism.
- Krebs, C. J., S. Boutin, R. Boonstra, A. R. E. Sinclair, J. N. M. Smith, M. R. T. Dale, K. Martin, and R. Turkington. 1993. Impact of food and predation on the snowshoe hare cycle. Science 269:1112-1115.
- May, Robert and Angela McLean, (Editors). 2007. Theoretical Ecology: Principles and Applications. New York: Oxford University Press. ISBN: 0199209995.
- Real, Leslie A. and James H. Brown, (Editors). 1991. Foundations of Ecology: Classic Papers with Commentaries. Chicago: University of Chicago Press. Volterra’s paper is included (page 283) and there are other papers and commentaries which are of interest to predator-prey dynamics. ISBN: 0226705943.