Maximum power principle
| Topics: |
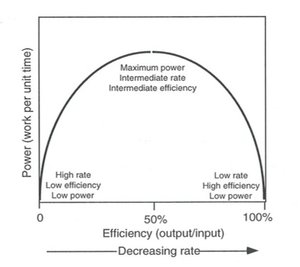
Odum used and elaborated Lotka’s energy principle as an evolutionary criterion in systems. He clearly differentiated between energy efficiency (the ratio of useful outputs over total inputs) in systems and power (the rate of doing useful work) and related these two concepts[1]. As Figure 1 shows, at zero efficiency power is also zero because no work is being done. But at maximum efficiency, power again is zero because to achieve maximum efficiency one has to run processes reversibly, which for thermodynamic systems means infinitely slowly. Therefore the rate of doing work goes to zero. It is at some intermediate efficiency (where one is “wasting” a large percentage of the energy) that power is maximized. Consider a simple example: the Atwood’s machine. Here an elevated weight attached to one end of a line over a pulley is used to pull up another weight attached to the other end of the line. When there is no weight at all attached to the lower end, the upper weight descends very rapidly but no work has been done because nothing has been lifted. We are at the zero efficiency side of Figure 1. When a weight exactly equal to the elevated weight is attached to the lower end, the system is at maximum efficiency in Figure 1 but again the rate of doing work is zero because the lower weight doesn’t move because the weights are perfectly balanced. When the lower weight is at 50% of the upper weight, the system maximizes the rate of doing work or power, as shown in Figure 1. The significance of this is that in systems (including both ecological and economic systems), those configurations that maximize power, not efficiency, will be at a selective advantage. Entropy dissipation is required for the survival of living systems and there are limits to the efficiency at which this can go on in dynamic adaptive systems. These efficiency limits are at a much lower levels than those theoretically possible at reversible (i.e., infinitely slow) rates. For example, real power plants operate much closer to the maximum power efficiency than to the maximum possible efficiency.
Notes
This Informational Box is an excerpt from An Introduction to Ecological Economics by Robert Costanza, John H Cumberland, Herman Daly, Robert Goodland, Richard B Norgaard. ISBN: 1884015727