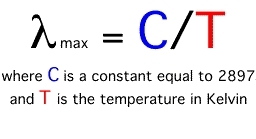Electromagnetic radiation
| Topics: |
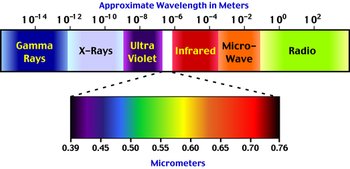 Figure 1: Some of the various types of electromagnetic radiation as defined by Wavelength. Visible light has a spectrum that ranges from 0.40 to 0.71 micrometers (µm). (Source: PhysicalGeography.net)
Figure 1: Some of the various types of electromagnetic radiation as defined by Wavelength. Visible light has a spectrum that ranges from 0.40 to 0.71 micrometers (µm). (Source: PhysicalGeography.net) Radiation (from Latin radiare, 'to emit beams') is energy transmitted through space as particles or electromagnetic waves or the process of their emission. All objects above the temperature of absolute zero (-273.15° Celsius) radiate energy to their surrounding environment. Particle radiation refers to the radiation of energy by means of small, fast-moving particles that have energy and mass. Electromagnetic radiation is emitted in discrete units known as photons that travel at the speed of light as electromagnetic waves. Electromagnetic energy is classified by increasing energy or decreasing wavelength into radio waves, microwaves, infrared, visible light, ultraviolet, X-rays and gamma-rays (Figure 1).
Radiation is separated into two categories, ionizing and non-ionizing, to denote the energy and danger of the radiation. Ionizing radiation is radiation in which an individual particle carries enough energy to ionize an atom or molecule. Corpuscular ionizing radiation consists of fast-moving, charged particles such as electrons, positrons, or small atomic nuclei. Thermal, epithermal, and fast neutrons interact with atomic nuclei creating secondary ionizing radiation and are called indirectly ionizing radiation. Electromagnetic ionizing radiation includes X-rays and gamma-rays. Ultraviolet light also can ionize an atom or molecule, but is referred to usually as non-ionizing radiation. The amount of ionizing radiation, or 'absorbed dose' is measured in grays. One gray (Gy) is one joule of the energy deposited per kilogram of mass. Some types of radiation, such as neutrons or alpha particles, are more biologically damaging than photons or fast electrons when the absorbed dose from both is equal. To estimate this, dose equivalent, in a unit called the sievert (Sv), is used. Regardless of the type of radiation, one sievert of radiation produces the same biological effect. High radiation doses tend to kill cells, while low doses tend to damage or alter the genetic code of irradiated cells. The effect of very low doses is a subject of current debate.
Visible light is a form of electromagnetic radiation that can be perceived by our eyes. Light has a wavelength of between 0.40 to 0.71 micrometers (µm). Figure 1 illustrates the various spectral color bands that make up light. The sun emits only a portion (44%) of its radiation in this zone. Solar radiation spans a spectrum from approximately 0.1 to 4.0 micrometers. The band from 0.1 to 0.4 micrometers is called ultraviolet radiation. About 7% of the sun's emission is in this wavelength band. About 48% of the sun's radiation falls in the region between 0.71 to 4.0 micrometers. This band is called the near (0.71 to 1.5 micrometers) and far (1.5 to 4.0 micrometers) infrared .
The amount of electromagnetic radiation emitted by a body is directly related to its temperature. If the body is a perfect emitter (black body), the amount of radiation given off is proportional to the 4th power of its temperature as measured in Kelvin units. This natural phenomenon is described by the Stephan-Boltzmann Law. The following simple equation describes this law mathematically:
According to the Stephan-Boltzmann equation, a small increase in the temperature of a radiating body results in a large amount of additional radiation being emitted.
In general, good emitters of radiation are also good absorbers of radiation at specific wavelength bands. This is especially true of gases and is responsible for the Earth's greenhouse effect. Likewise, weak emitters of radiation are also weak absorbers of radiation at specific wavelength bands. This fact is referred to as Kirchhoff's Law. Some objects in nature have almost completely perfect abilities to absorb and emit radiation. We call these objects black bodies. The radiation characteristics of the sun and the Earth are very close to being black bodies.
The wavelength of maximum emission of any body is inversely proportional to its absolute temperature. Thus, the higher the temperature, the shorter the wavelength of maximum emission. This phenomenon is often called Wien's Law. The following equation describes this law:
Wien's Law suggests that as the temperature of a body increases, the wavelength of maximum emission becomes smaller. According to the above equation, the wavelength of maximum emission for the sun (5,800 [[Kelvin]s]) is about 0.5 micrometers, while the wavelength of maximum emission for the Earth (288 Kelvins) is approximately 10.0 micrometers.
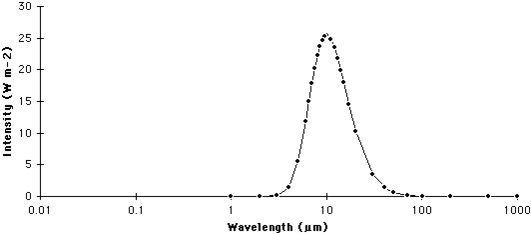
A graph that describes the quantity of radiation that is emitted from a body at particular wavelengths is commonly called a spectrum. The following two graphs describe the spectrums for the sun and Earth (Figure 2 and Figure 3).
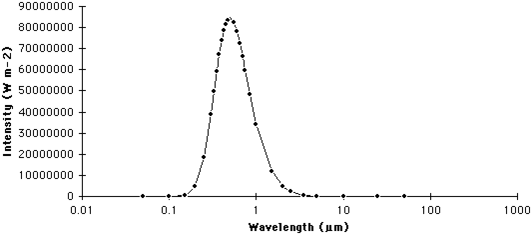 Figure 4: Diagram illustrating the diffusion of radiation due to the Inverse Square Law. (Source: PhysicalGeography.net) Figure 4: Diagram illustrating the diffusion of radiation due to the Inverse Square Law. (Source: PhysicalGeography.net)
|
|
Figure 4: Diagram illustrating the diffusion of radiation due to the Inverse Square Law. (Source: PhysicalGeography.net) |
The graphs in Figures 2 and 3 illustrate two important points concerning the relationship between the temperature of a body and its emissions of electromagnetic radiation:
- The amount of radiation emitted from a body increases exponentially with a linear rise in temperature (see above Stephan-Boltzmann's Law).
- The average wavelength of electromagnetic emissions becomes shorter with increasing temperature (see above Wien's Law).
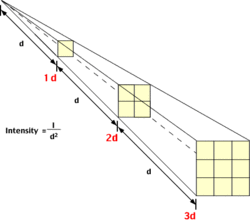
Finally, the amount of radiation passing through a specific area is inversely proportional to the square of the distance of that area from the energy source. This phenomenon is called the Inverse Square Law. Using this law we can model the effect that distance traveled has on the intensity of emitted radiation from a body like the sun. Figure 4 suggests that the intensity of radiation emitted by a body quickly diminishes with distance in a nonlinear fashion.
Mathematically, the Inverse Square Law is described by the equation:
where I is the intensity of the radiation at 1d (see Figure 4) and d is the distance traveled.
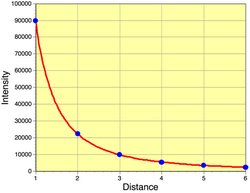
The decrease in intensity with distance is not linear when graphed (Figure 5).
Further Reading