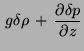Beta plane approximation
The beta plane approximation, in oceanography and general fluid dynamics, is a simplified coordinate system for the equations of motion where the variation of the Coriolis parameterf with latitude is approximated by
where f0 is the value of f at the mid-latitude of the region and β the latitudinal gradient of f at that same latitude. This formalism is used to investigate both equatorial and mid-latitude phenomena (for which there are slightly different beta plane approximations) where f varies significantly over a few tens of degrees latitude. The beta plane approximation allows considerable simplification of the governing equations and therefore the use of analytical investigation methods. See Gill [1982].
The beta plane equations are obtained by introducing a background stratification into the shallow water equations, expanding them around a reference latitude θ0 with respect to ε~ θ − θ0, and keeping terms up to first order in ". This approximation introduces the horizonal coordinates
and expands the Coriolis parameter as
where β0 is the beta paramter at the reference latitude. The resulting equations (after Muller [1995])
are:
![]() Image:Img62.png +
Image:Img62.png + 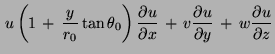 Image:Img64.png -
Image:Img64.png - ![]() Image:Img66.png =
Image:Img66.png = 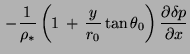 Image:Img67.png
Image:Img67.png
![]() Image:Img68.png +
Image:Img68.png + 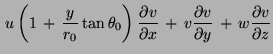 Image:Img69.png +
Image:Img69.png + 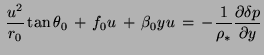 Image:Img70.png
Image:Img70.png
![]() Image:Img73.png =
Image:Img73.png = 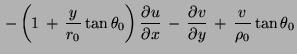 Image:Img74.png
Image:Img74.png
![]() Image:Img75.png +
Image:Img75.png + 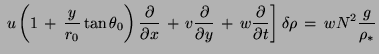 Image:Img76.png
Image:Img76.png
where (u, v,w) are the velocity components in the (x, y, z) directions, r0 is the mean radius of the Earth, θ0 is the reference latitude, f0 = 2Ωsin θ0 is the Coriolis parameter at the reference latitude, 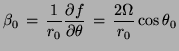 Image:Img81.png is the beta parameter at the reference latitude, ρ* is a constant reference density, δp and δρ are motionally induced deviations from prescribed background fields, and N is the buoyancy frequency.
Image:Img81.png is the beta parameter at the reference latitude, ρ* is a constant reference density, δp and δρ are motionally induced deviations from prescribed background fields, and N is the buoyancy frequency.
| This article is written at a definitional level only. Authors wishing to expand this entry are inivited to expand the present treatment, which additions will be peer reviewed prior to publication of any expansion. |
Further Reading
- J.R.Holton. 2004. An introduction to dynamical meteorology, Academic Press. ISBN 978-0123540157.
- Physical Oceanography Index