Differential Equations, Parametric Equations, and Sequences and Series

Differential equations are solved by finding the function for which the equation holds true.

Differential equations can be used to model a variety of physical systems.

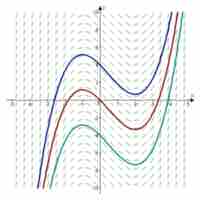
Direction fields and Euler's method are ways of visualizing and approximating the solutions to differential equations.

Separable differential equations are equations wherein the variables can be separated.

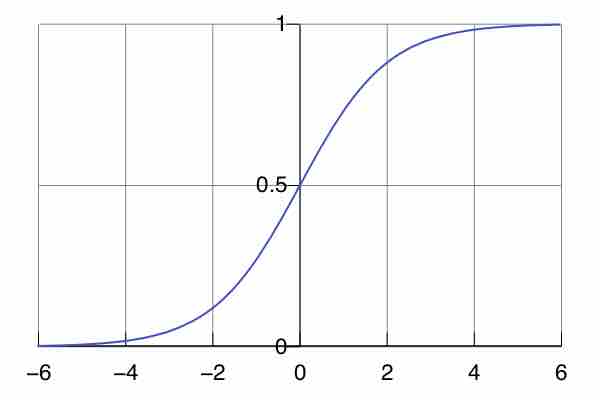
A logistic equation is a differential equation which can be used to model population growth.

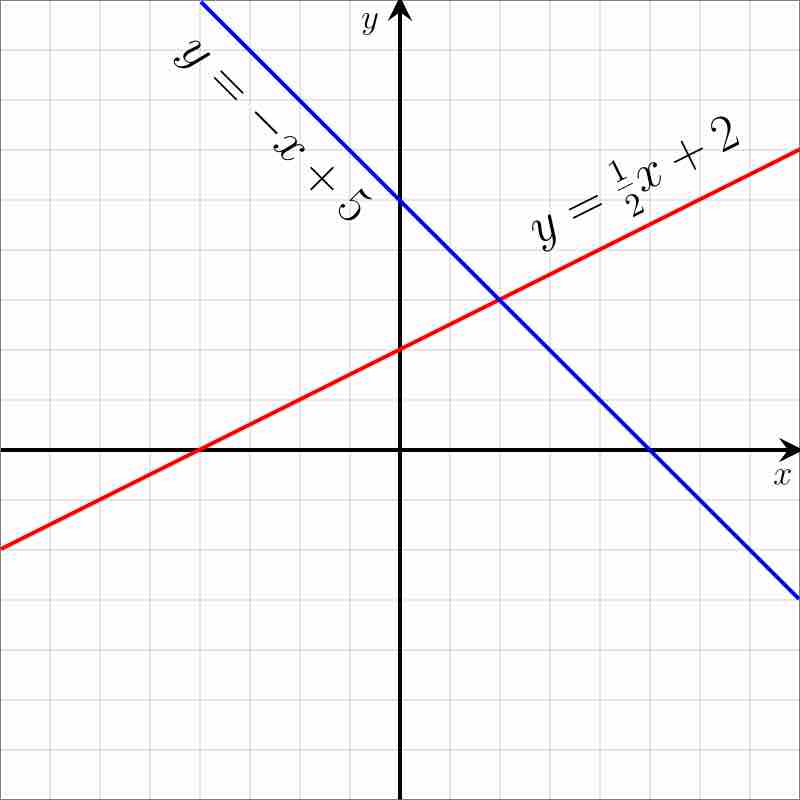
Linear equations are equations of a single variable.

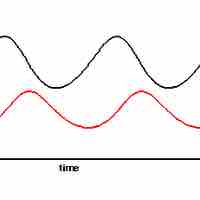
The relationship between predators and their prey can be modeled by a set of differential equations.

Parametric equations are a set of equations in which the coordinates (e.g., $x$ and $y$) are expressed in terms of a single third parameter.

Calculus can be applied to parametric equations as well.

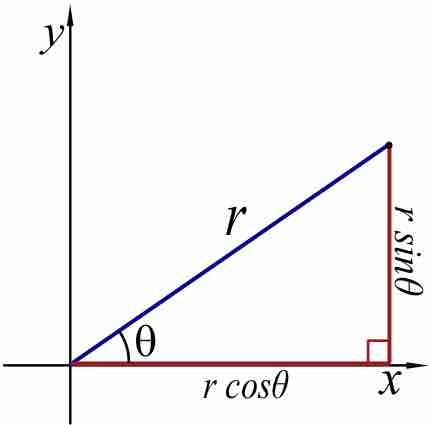
Polar coordinates define the location of an object in a plane by using a distance and an angle from a reference point and axis.

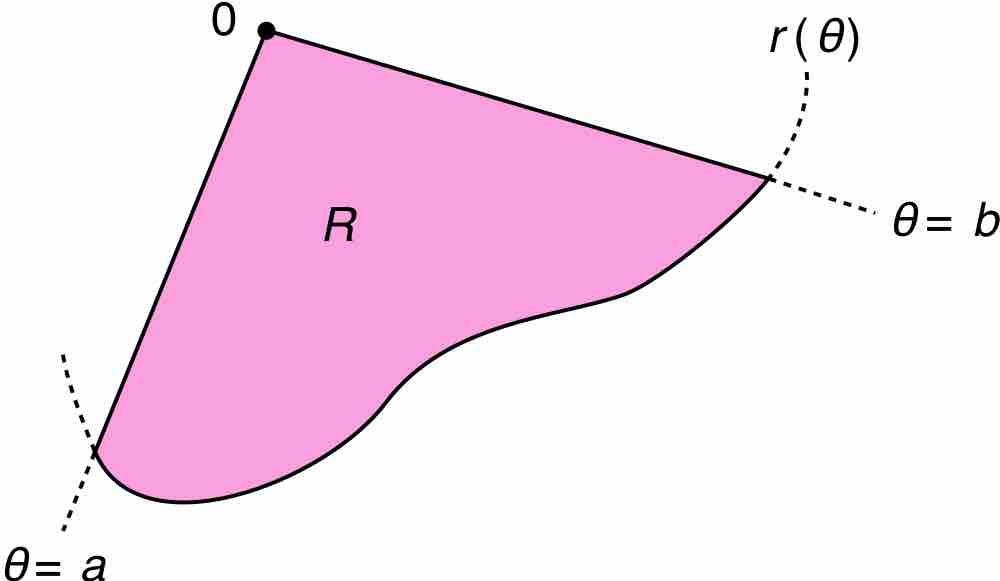
Area and arc length are calculated in polar coordinates by means of integration.

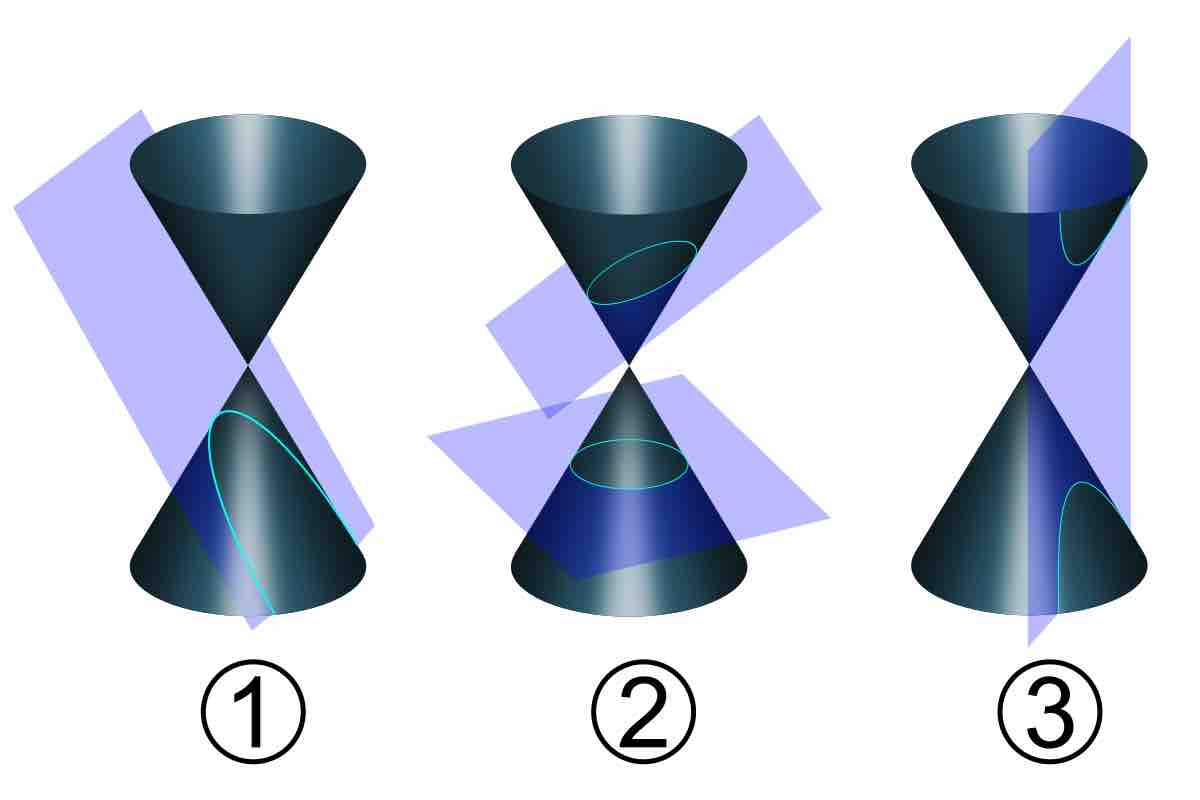
Conic sections are defined by intersections of cones with planes.

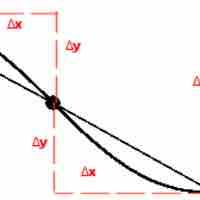
Arc length and speed in parametric equations can be calculated using integration and the Pythagorean theorem.

Conic sections are sections of cones and can be represented by polar coordinates.

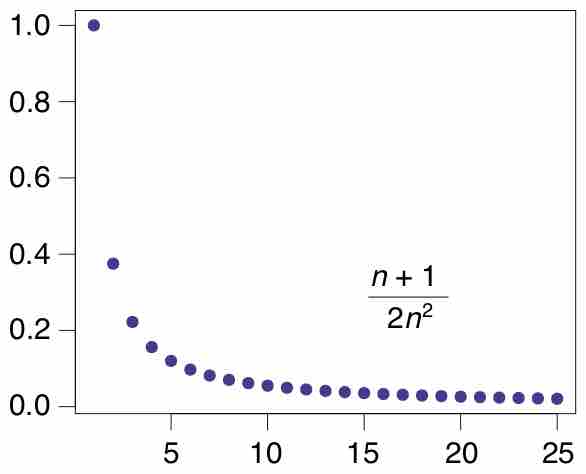
A sequence is an ordered list of objects and can be considered as a function whose domain is the natural numbers.

A series is the sum of the terms of a sequence.

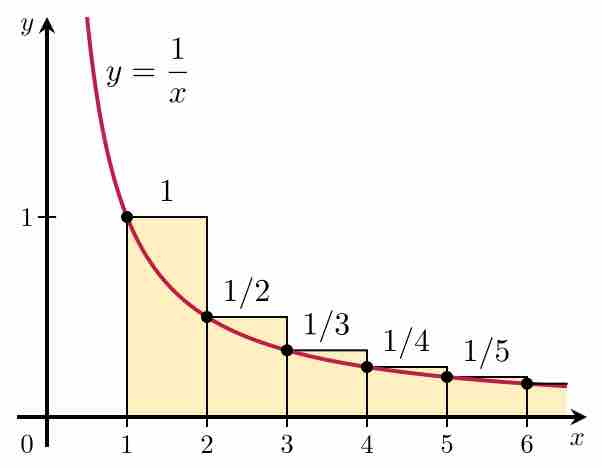
The integral test is a method of testing infinite series of nonnegative terms for convergence by comparing them to an improper integral.

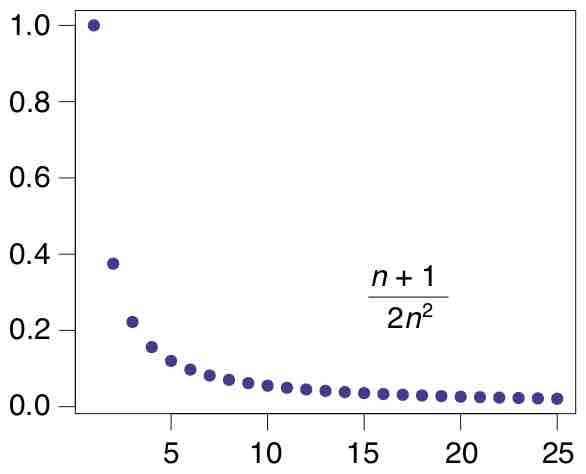
Comparison test may mean either limit comparison test or direct comparison test, both of which can be used to test convergence of a series.

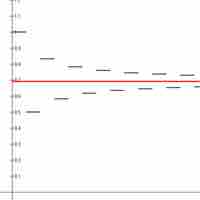
An alternating series is an infinite series of the form $\sum_{n=0}^\infty (-1)^n\,a_n$ or $\sum_{n=0}^\infty (-1)^{n-1}\,a_n$ with $a_n > 0$ for all $n$.

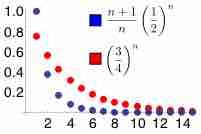
An infinite series of numbers is said to converge absolutely if the sum of the absolute value of the summand is finite.

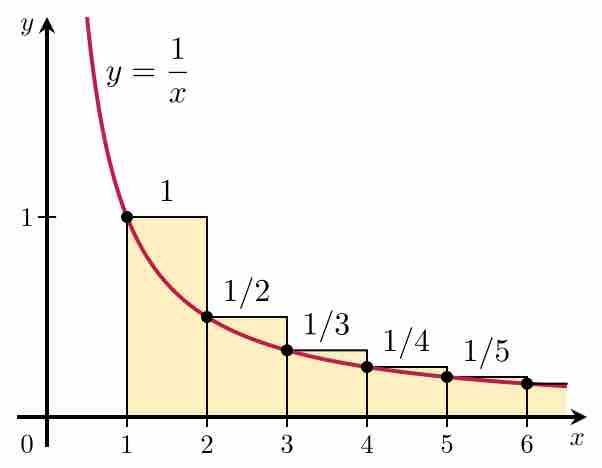
Convergence tests are methods of testing for the convergence or divergence of an infinite series.

A power series (in one variable) is an infinite series of the form $f(x) = \sum_{n=0}^\infty a_n \left( x-c \right)^n$, where $a_n$ is the coefficient of the $n$th term and $x$ varies around $c$.

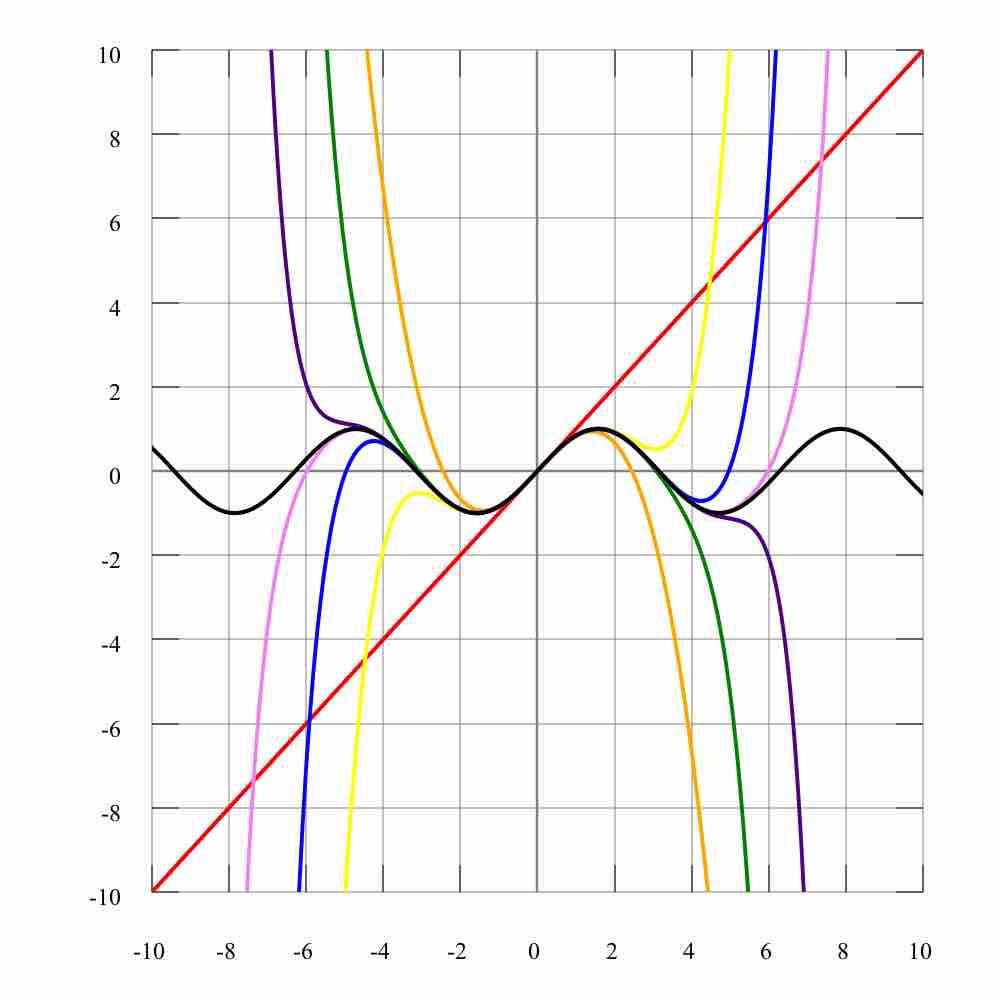
A power function is a function of the form $f(x) = cx^r$ where $c$ and $r$ are constant real numbers.

Taylor series represents a function as an infinite sum of terms calculated from the values of the function's derivatives at a single point.

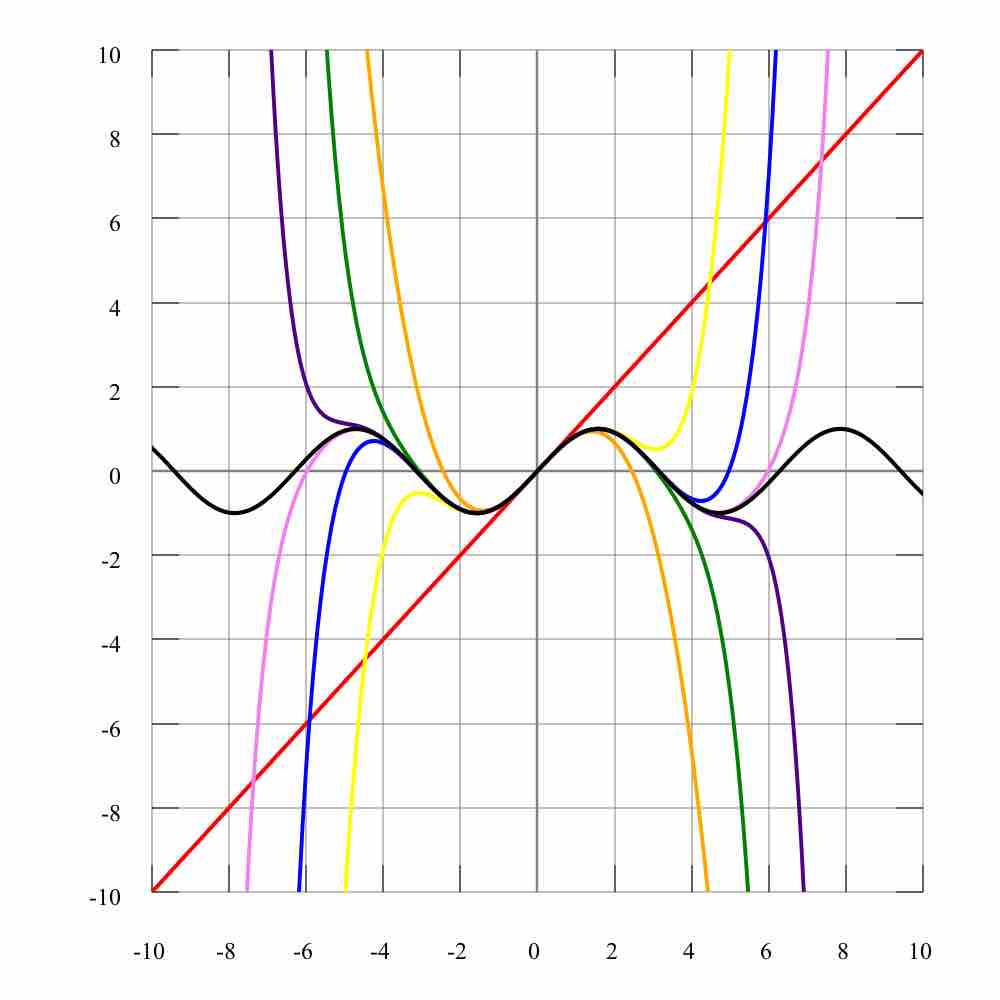
Taylor series expansion can help approximating values of functions and evaluating definite integrals.

Infinite sequences and series can either converge or diverge.

For a sequence $\{a_n\}$, where $a_n$ is a non-negative real number for every $n$, the sum $\sum_{n=0}^{\infty}a_n$ can either converge or diverge to $\infty$.