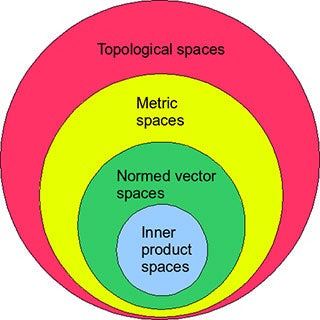
A hierarchy of mathematical spaces: The inner product induces a norm. The norm induces a metric. The metric induces a topology. (Image by Jhausauer,on Wikimedia Commons. Public domain.)
Instructor(s)
Dr. Casey Rodriguez
MIT Course Number
18.102 / 18.1021
As Taught In
Spring 2021
Level
Undergraduate / Graduate
Course Description
Course Features
Course Description
Functional analysis helps to solve problems where the vector space is no longer finite-dimensional, a situation that arises very naturally in many concrete problems. Topics will include normed spaces, completeness, functionals, Hahn-Banach theorem, duality, operators; Lebesgue measure, measurable functions, integrability, completeness of Lp spaces; Hilbert spaces; compact and self-adjoint operators; and the spectral theorem.
Other Versions
Other OCW Versions
OCW has published multiple versions of this subject. ![]()


