Non-Conservative Forces

Example 7.10 Calculating Distance Traveled: Sliding Up an Incline

Suppose that the player from Example 7.9 is running up a hill having a $5.00^{\circ}$ incline upward with a surface similar to that in the baseball stadium. The player slides with the same initial speed, and the frictional force is still 450 N. Determine how far he slides.

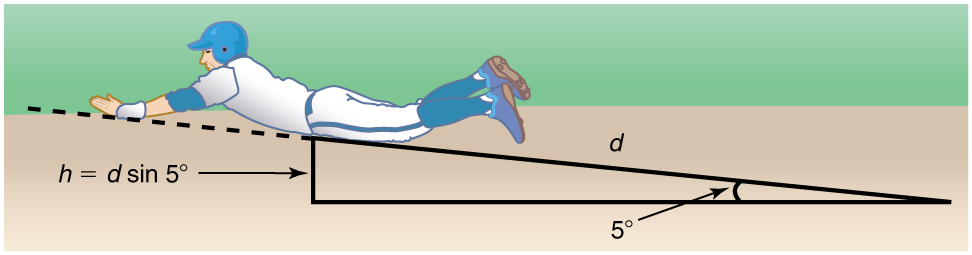
Figure 7.18 The same baseball player slides to a stop on a $5.00^{\circ}$ slope.

Strategy

In this case, the work done by the nonconservative friction force on the player reduces the mechanical energy he has from his kinetic energy at zero height, to the final mechanical energy he has by moving through distance $d$ to reach height $h$ along the hill, with $h=d \sin 5.00^{\circ}$. This is expressed by the equation

$\mathrm{KE}_{\mathrm{i}}+\mathrm{PE}_{\mathrm{i}}+W_{\mathrm{nc}}=\mathrm{KE}_{\mathrm{f}}+\mathrm{PE}_{\mathrm{f}}$.

Solution

The work done by friction is again $W_{\mathrm{nc}}=-f d$ ; initially the potential energy is $\mathrm{PE}_{\mathrm{i}}=m g \cdot 0=0$  and the kinetic energy is $\mathrm{KE}_{\mathrm{i}}=\frac{1}{2} m v_{\mathrm{i}}^{2}$; the final energy contributions are $\mathrm{KE}_{\mathrm{f}}=0$  for the kinetic energy and $\mathrm{PE}_{\mathrm{f}}=m g h=m g d \sin \theta$  for the potential energy.

Substituting these values gives

$\frac{1}{2} m v_{\mathrm{i}}^{2}+0+(-f d)=0+m g d \sin \theta$.

Solve this for $d$ to obtain

$\begin{aligned} d &=\frac{\left(\frac{1}{2}\right) m v_{\mathrm{i}}^{2}}{f+m g \sin \theta} \\ &=\frac{(0.5)(65.0 \mathrm{~kg})(6.00 \mathrm{~m} / \mathrm{s})^{2}}{450 \mathrm{~N}+(65.0 \mathrm{~kg})\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right) \sin \left(5.00^{\circ}\right)} \\ &=2.31 \mathrm{~m} \end{aligned}$

Discussion

As might have been expected, the player slides a shorter distance by sliding uphill. Note that the problem could also have been solved in terms of the forces directly and the work energy theorem, instead of using the potential energy.

This method would have required combining the normal force and force of gravity vectors, which no longer cancel each other because they point in different directions, and friction, to find the net force.

You could then use the net force and the net work to find the distance $d$ that reduces the kinetic energy to zero. By applying conservation of energy and using the potential energy instead, we need only consider the gravitational potential energy $mgh$ , without combining and resolving force vectors. This simplifies the solution considerably.