A polynomial inequalityA mathematical statement that relates a polynomial expression as either less than or greater than another. is a mathematical statement that relates a polynomial expression as either less than or greater than another. We can use sign charts to solve polynomial inequalities with one variable.
Solve:
Solution:
Begin by finding the critical numbers. For a polynomial inequality in standard form, with zero on one side, the critical numbers are the roots. Because is given in its factored form the roots are apparent. Here the roots are: 0, −3, and 4. Because of the strict inequality, plot them using open dots on a number line.

In this case, the critical numbers partition the number line into four regions. Test values in each region to determine if f is positive or negative. Here we choose test values −5, −1, 2, and 6. Remember that we are only concerned with the sign (+ or −) of the result.
After testing values we can complete a sign chart.

The question asks us to find the values where , or where the function is negative. From the sign chart we can see that the function is negative for x-values in between 0 and 4.

We can express this solution set in two ways:
In this textbook we will continue to present solution sets using interval notation.
Answer:
Graphing polynomials such as the one in the previous example is beyond the scope of this textbook. However, the graph of this function is provided below. Compare the graph to its corresponding sign chart.

Certainly it may not be the case that the polynomial is factored nor that it has zero on one side of the inequality. To model a function using a sign chart, all of the terms should be on one side and zero on the other. The general steps for solving a polynomial inequality are listed in the following example.
Solve:
Solution:
Step 1: Obtain zero on one side of the inequality. In this case, subtract to obtain a polynomial on the left side in standard from.
Step 2: Find the critical numbers. Here we can find the zeros by factoring.
There are three solutions, hence, three critical numbers , 0, and 3.The strict inequality indicates that we should use open dots.

Step 3: Create a sign chart. In this case use and test values −2, −1, 1, and 4 to determine the sign of the function in each interval.
With this information we can complete the sign chart.

Step 4: Use the sign chart to answer the question. Here the solution consists of all values for which Shade in the values that produce positive results and then express this set in interval notation.

Answer:
Solve:
Solution:
Begin by rewriting the inequality in standard form, with zero on one side.
Next find the critical numbers of :
The critical numbers are −2, −1, and 2. Because of the inclusive inequality () we will plot them using closed dots.

Use test values −3, , 0, and 3 to create a sign chart.
And we have

Use the sign chart to shade in the values that have negative results ().

Answer:
A rational inequalityA mathematical statement that relates a rational expression as either less than or greater than another. is a mathematical statement that relates a rational expression as either less than or greater than another. Because rational functions have restrictions to the domain we must take care when solving rational inequalities. In addition to the zeros, we will include the restrictions to the domain of the function in the set of critical numbers.
Solve:
Solution:
The zeros of a rational function occur when the numerator is zero and the values that produce zero in the denominator are the restrictions. In this case,
Therefore the critical numbers are −2, 1, and 4. Because of the inclusive inequality () use a closed dot for the roots {−2, 4} and always use an open dot for restrictions {1}. Restrictions are never included in the solution set.

Use test values
And then complete the sign chart.

The question asks us to find the values for which , in other words, positive or zero. Shade in the appropriate regions and present the solution set in interval notation.

Answer:
Graphing such rational functions like the one in the previous example is beyond the scope of this textbook. However, the graph of this function is provided below. Compare the graph to its corresponding sign chart.
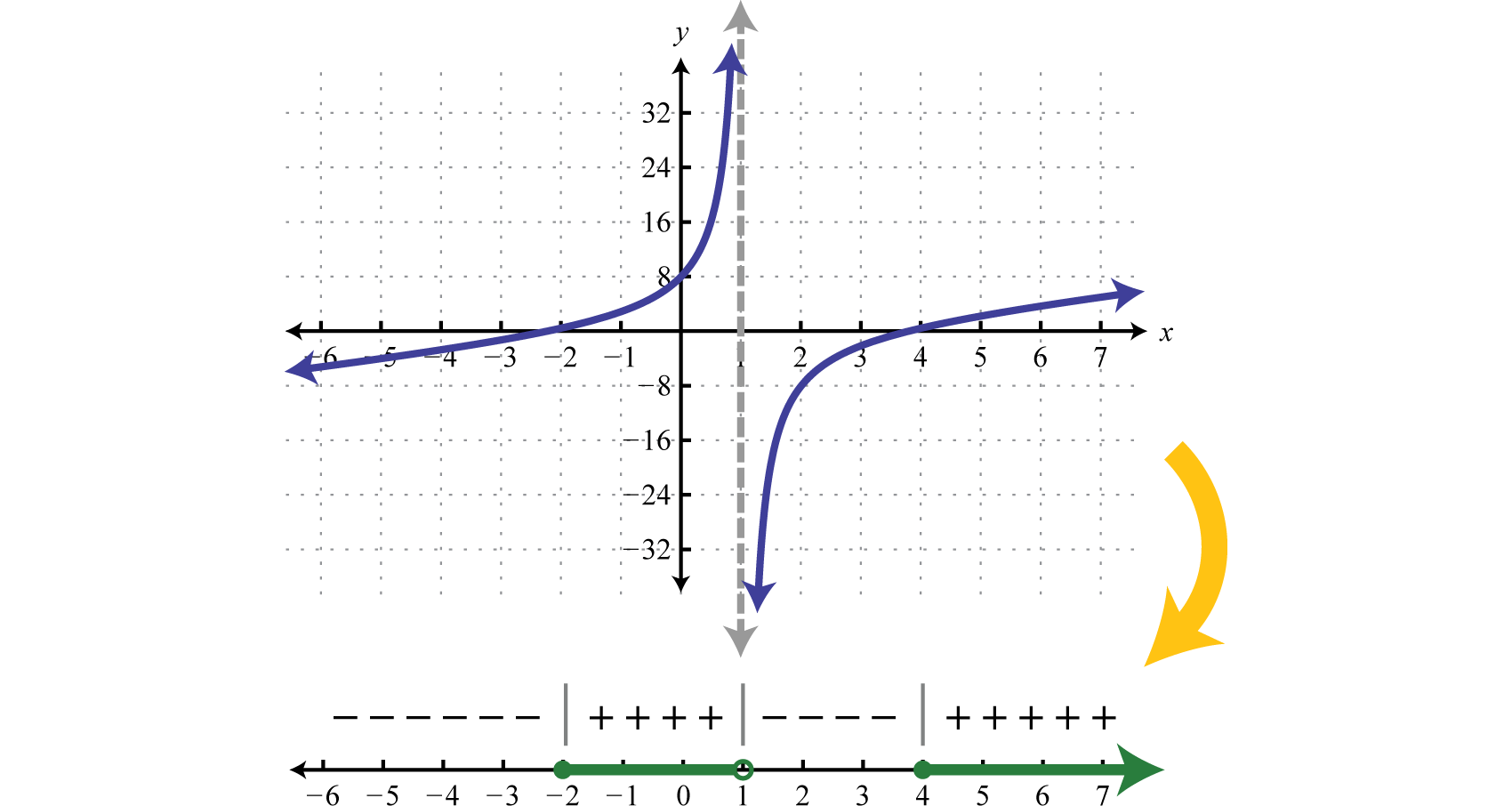
Notice that the restriction corresponds to a vertical asymptote which bounds regions where the function changes from positive to negative. While not included in the solution set, the restriction is a critical number. Before creating a sign chart we must ensure the inequality has a zero on one side. The general steps for solving a rational inequality are outlined in the following example.
Solve:
Solution:
Step 1: Begin by obtaining zero on the right side.
Step 2: Determine the critical numbers. The critical numbers are the zeros and restrictions. Begin by simplifying to a single algebraic fraction.
Next find the critical numbers. Set the numerator and denominator equal to zero and solve.
In this case, the strict inequality indicates that we should use an open dot for the root.
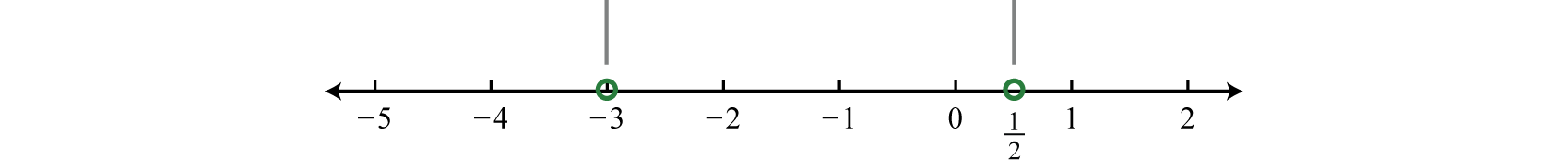
Step 3: Create a sign chart. Choose test values −4, 0, and 1.
And we have
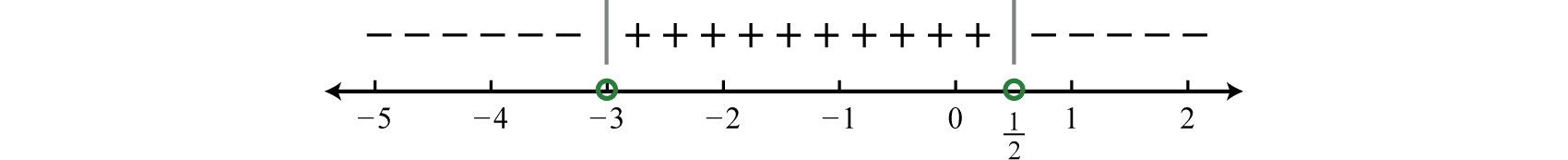
Step 4: Use the sign chart to answer the question. In this example we are looking for the values for which the function is negative, Shade the appropriate values and then present your answer using interval notation.
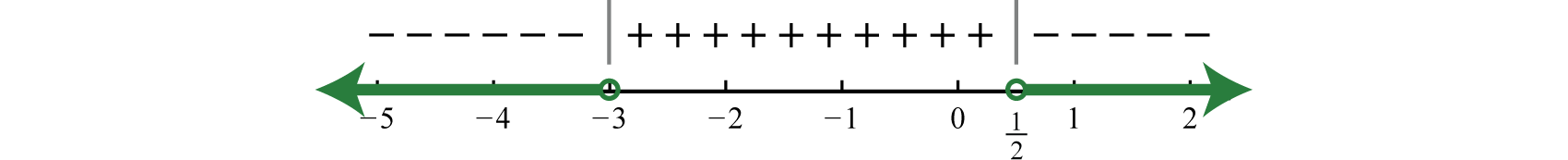
Answer:
Solve:
Solution:
Begin by obtaining zero on the right side.
Next simplify the left side to a single algebraic fraction.
The critical numbers are −3, −2, and 2. Note that ±2 are restrictions and thus we will use open dots when plotting them on a number line. Because of the inclusive inequality we will use a closed dot at the root −3.

Choose test values −4, , 0, and 3.
Construct a sign chart.

Answer the question; in this case, find x where

Answer:
Solve. Present answers using interval notation.
Solve.
Solve.
Solve.
Does the sign chart for any given polynomial or rational function always alternate? Explain and illustrate your answer with some examples.
Write down your own steps for solving a rational inequality and illustrate them with an example. Do your steps also work for a polynomial inequality? Explain.
Answer may vary