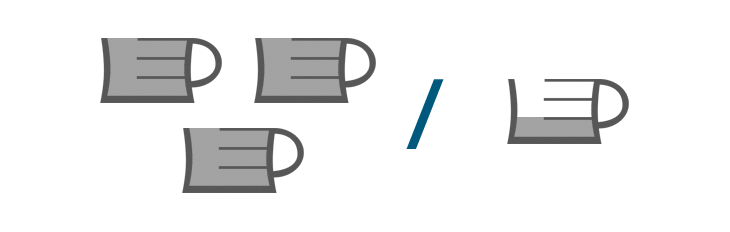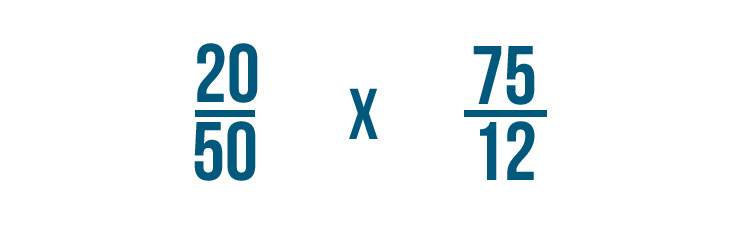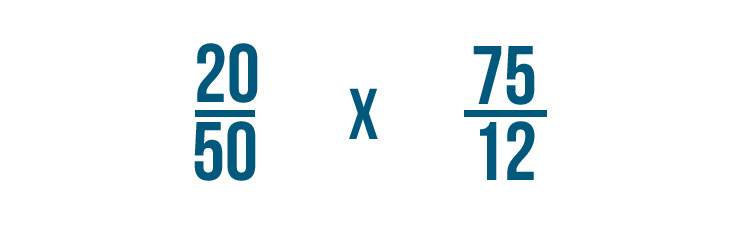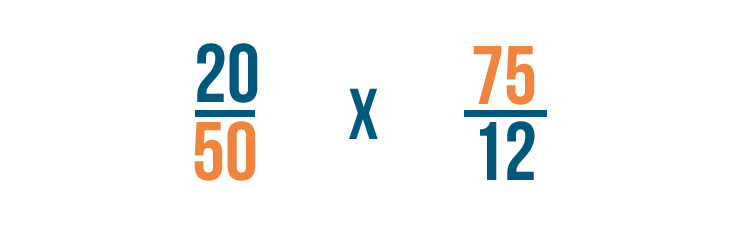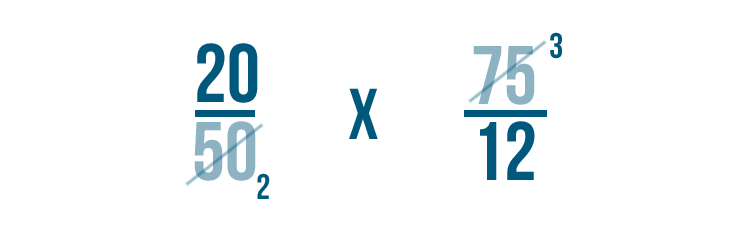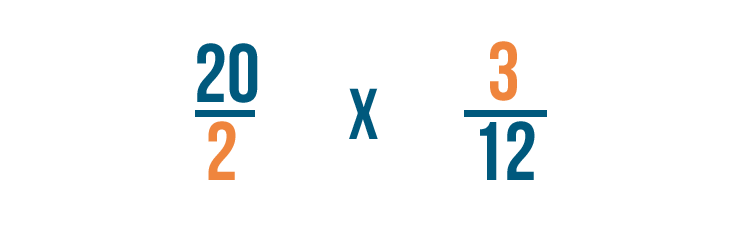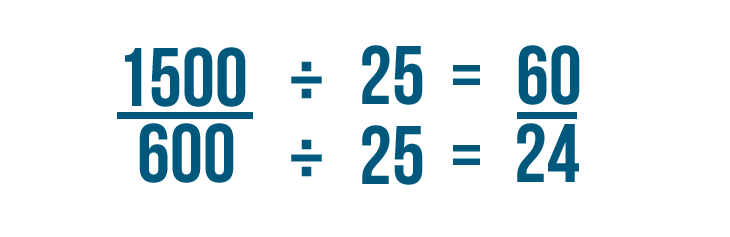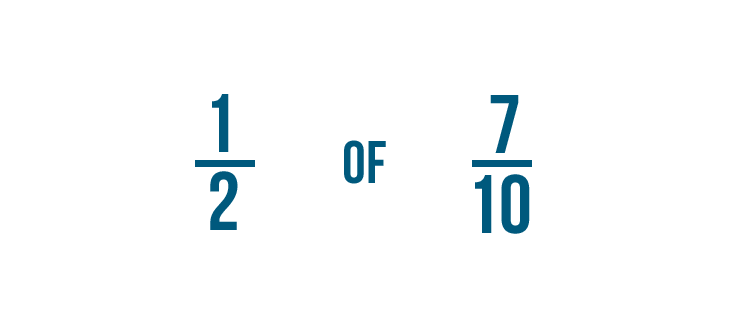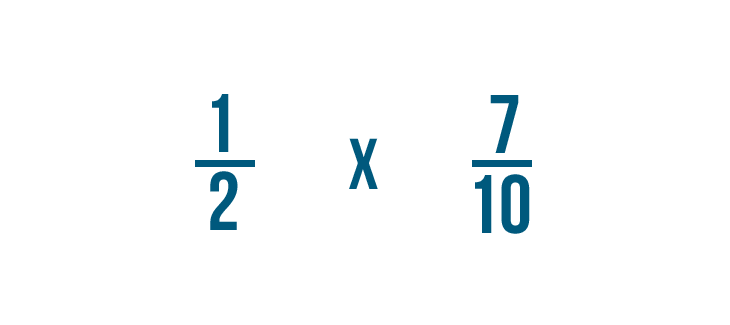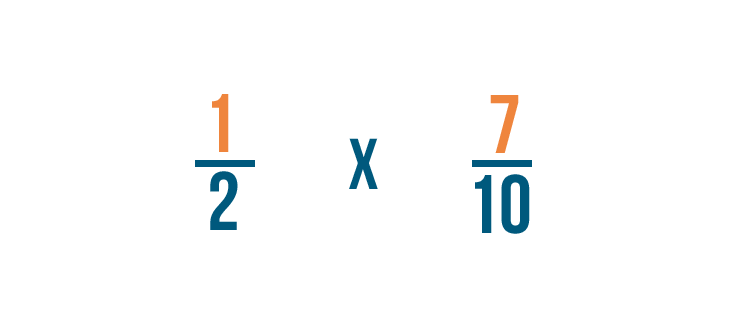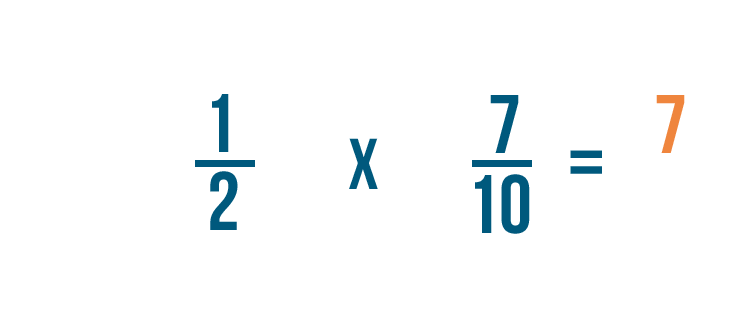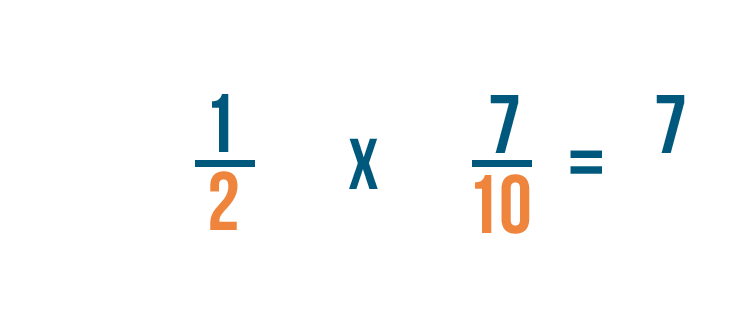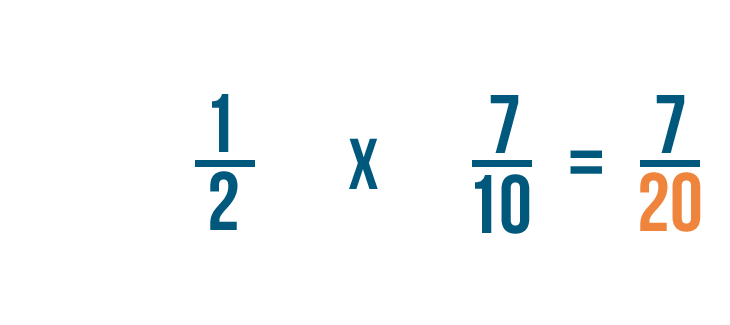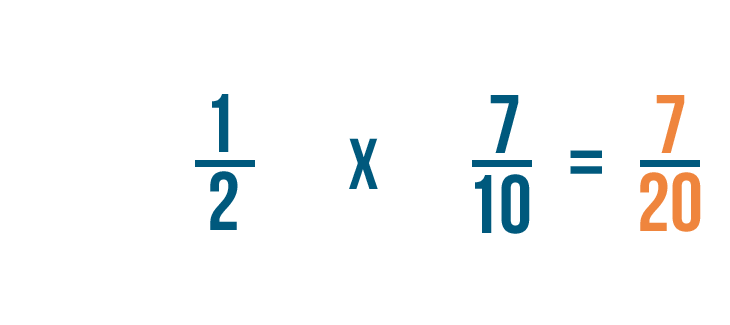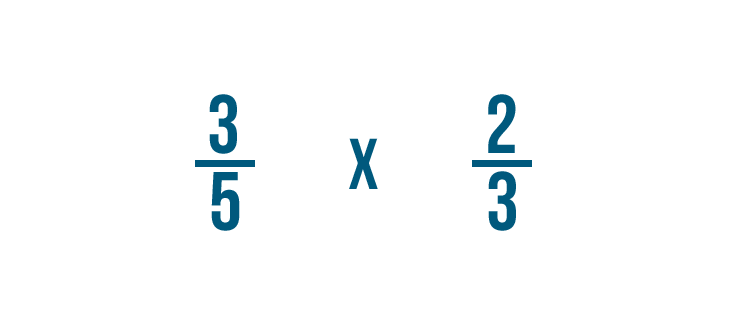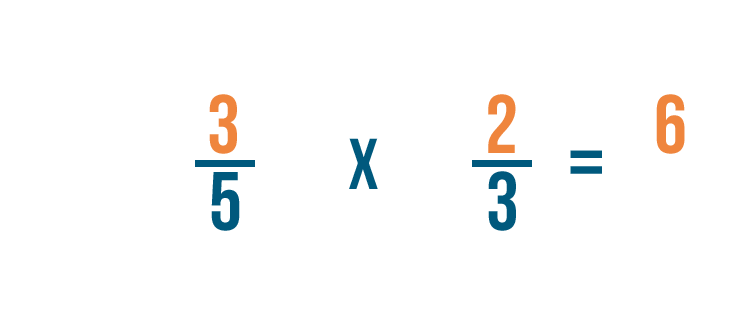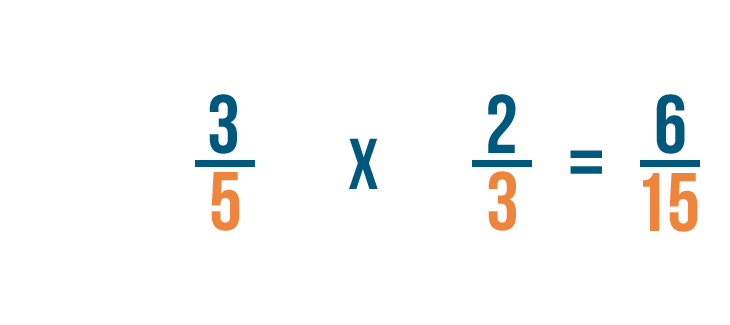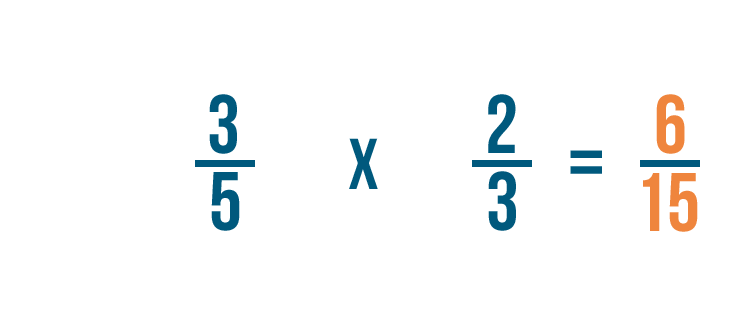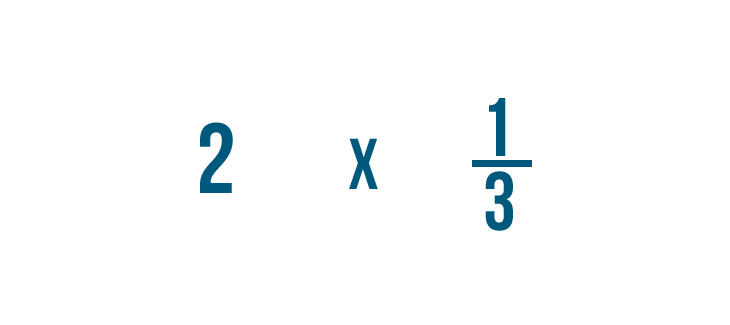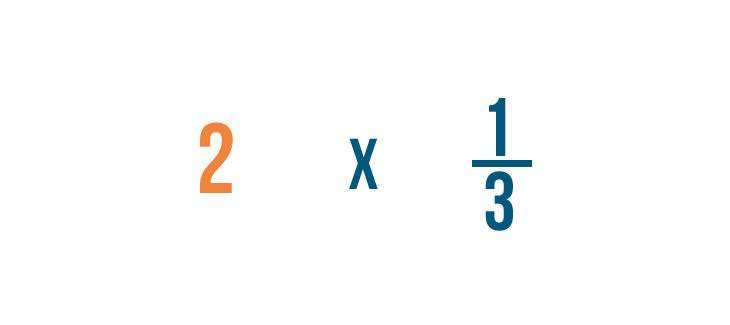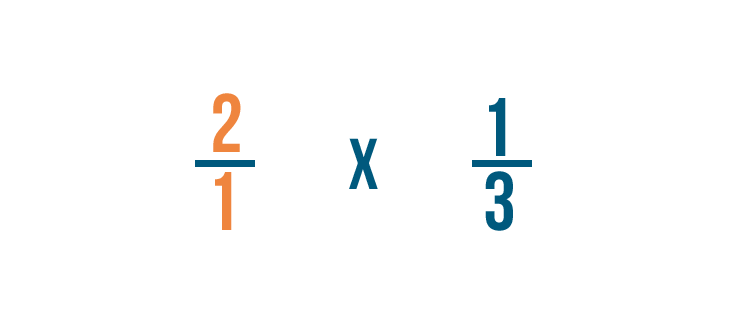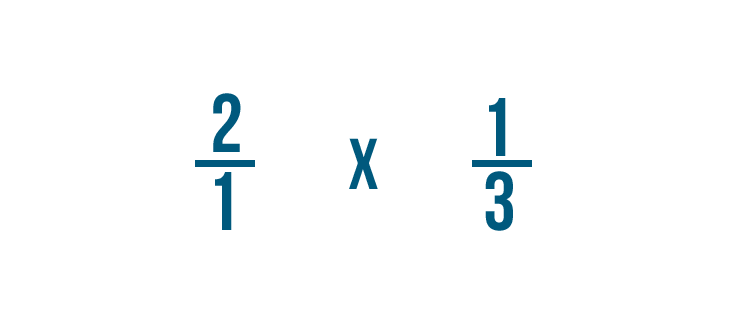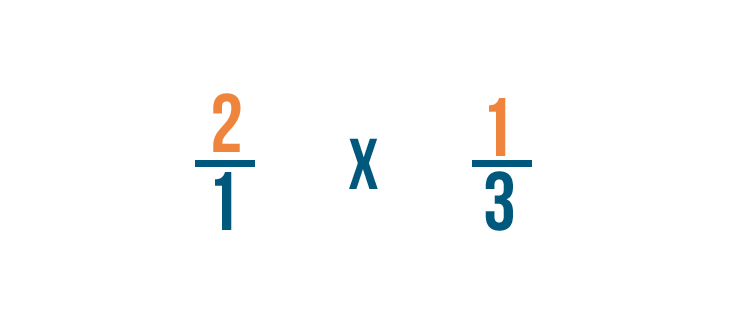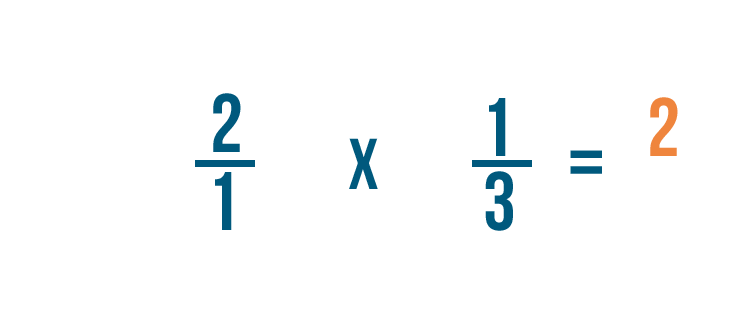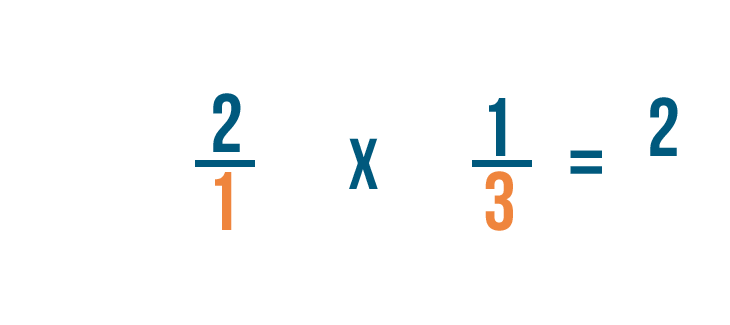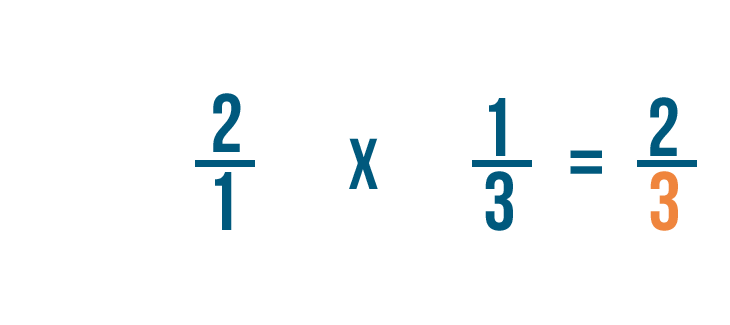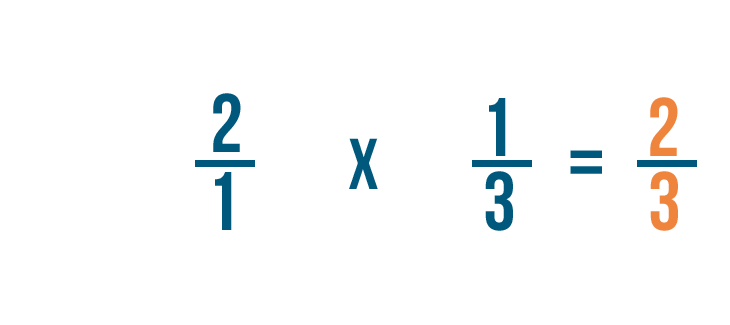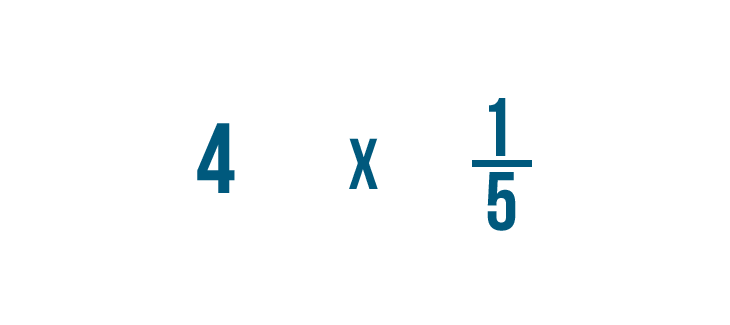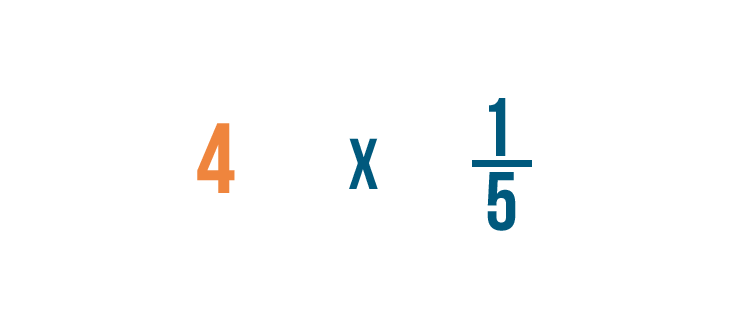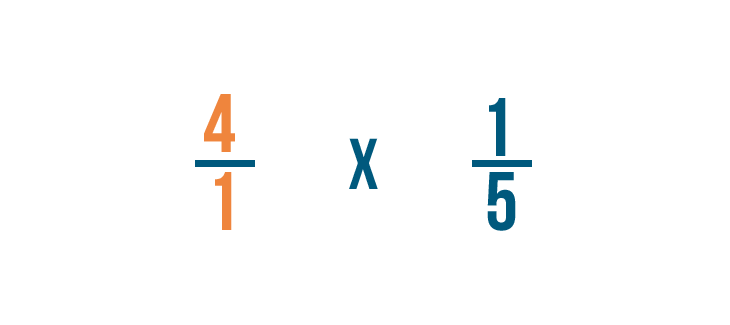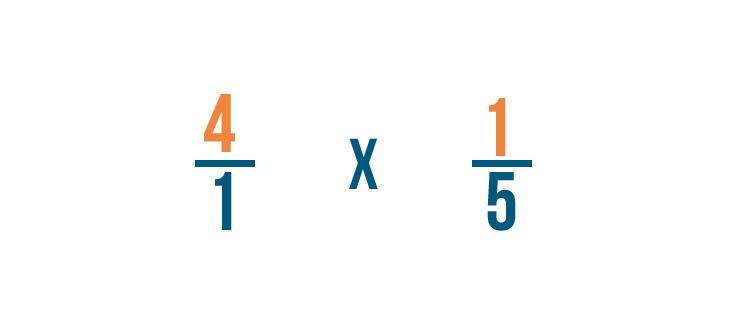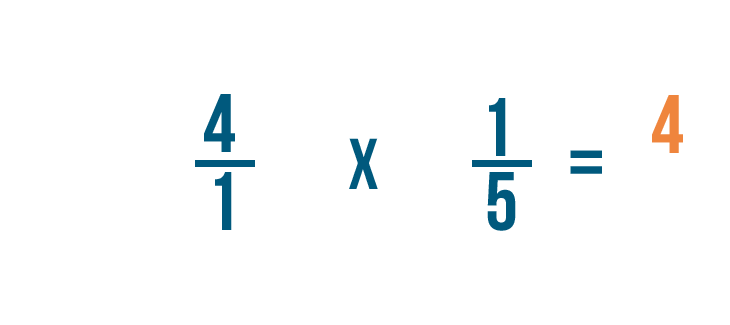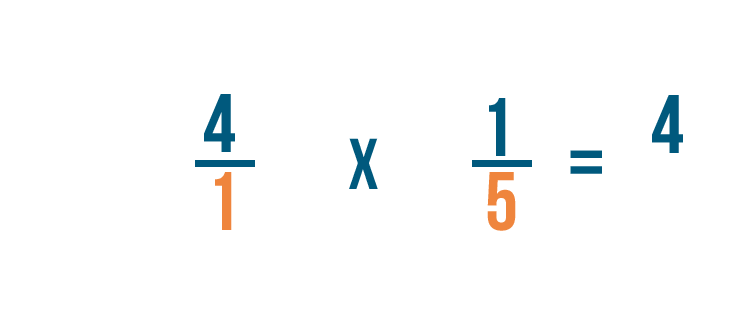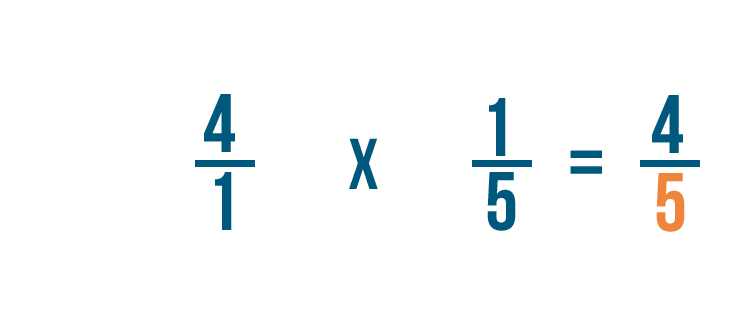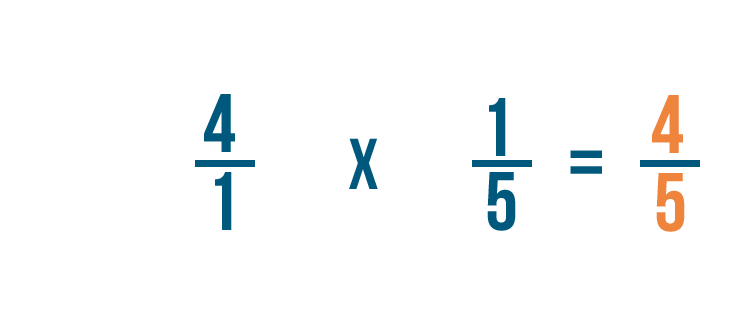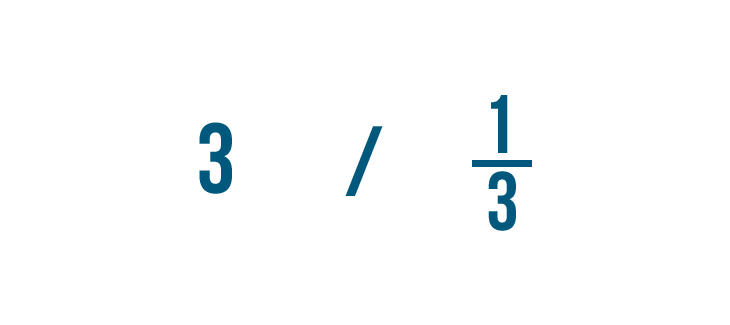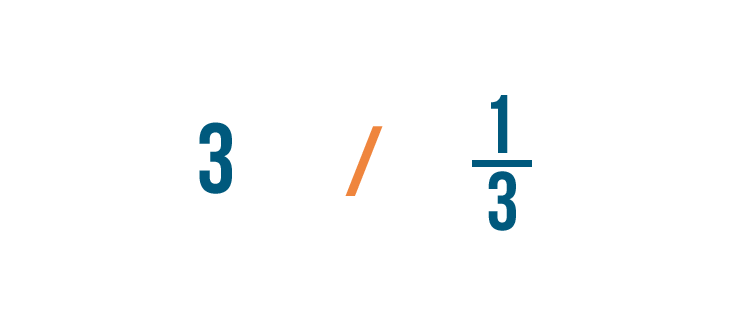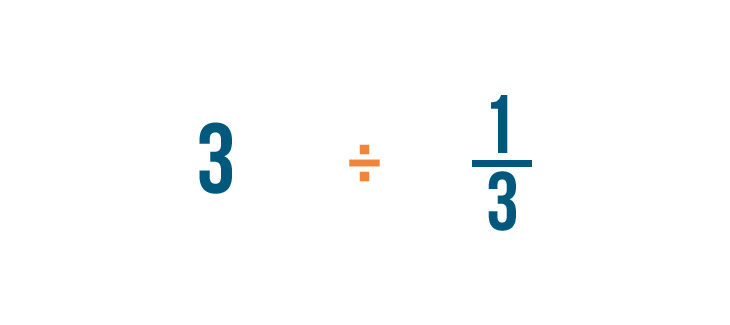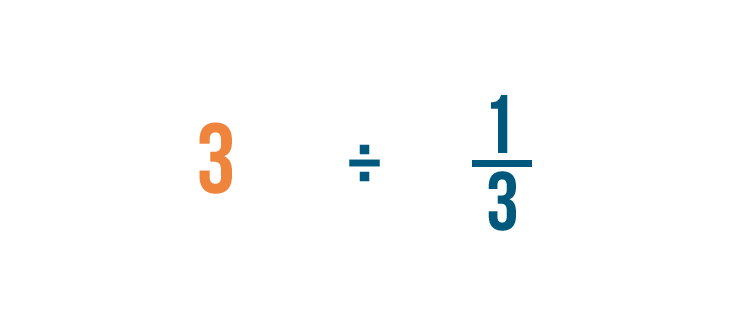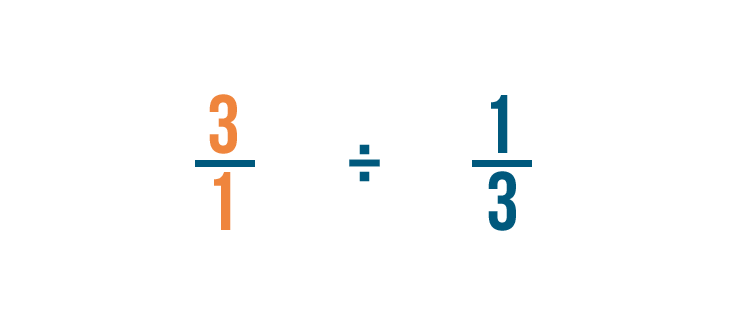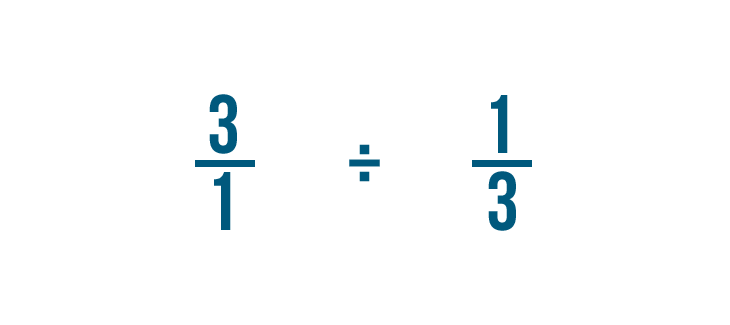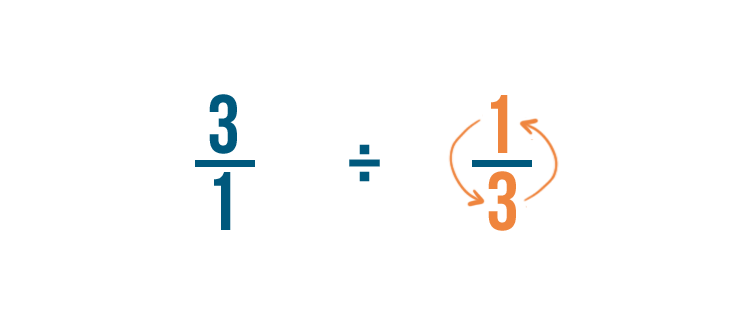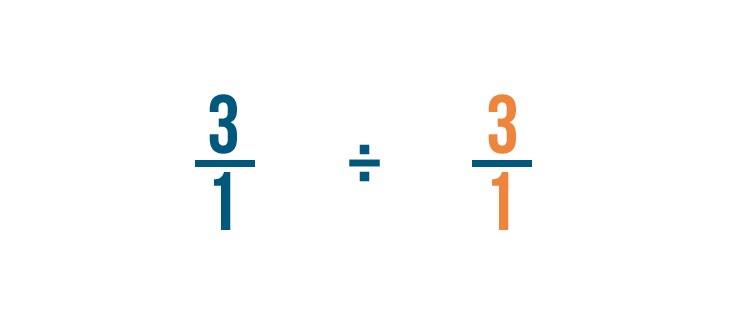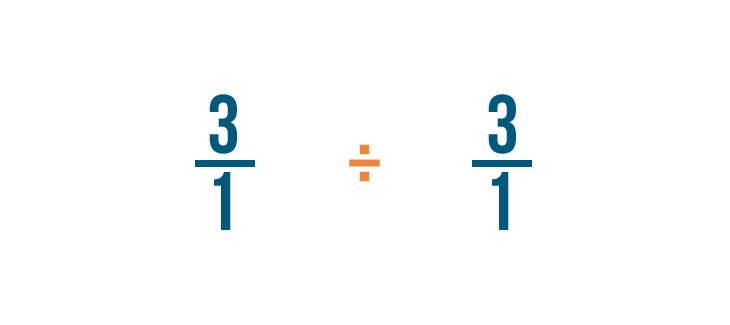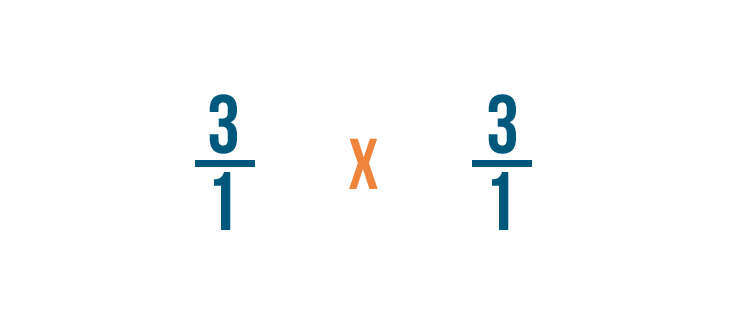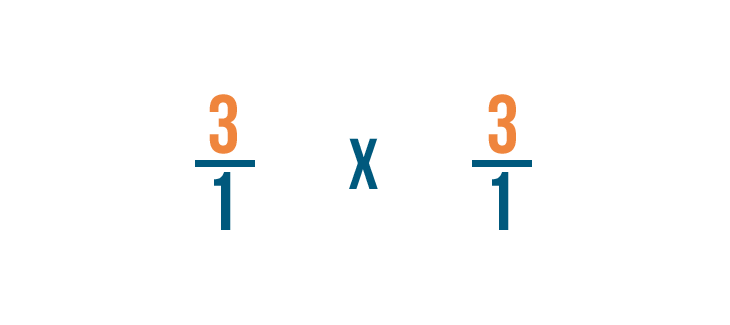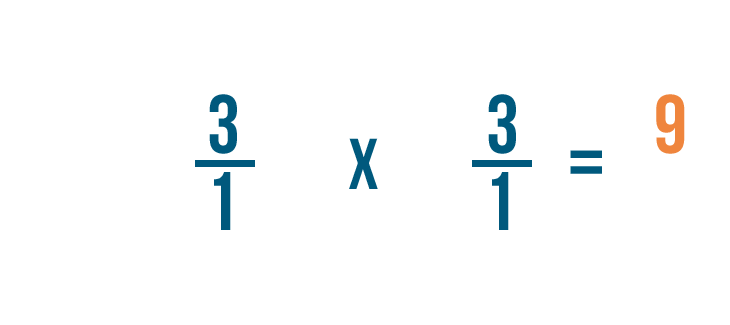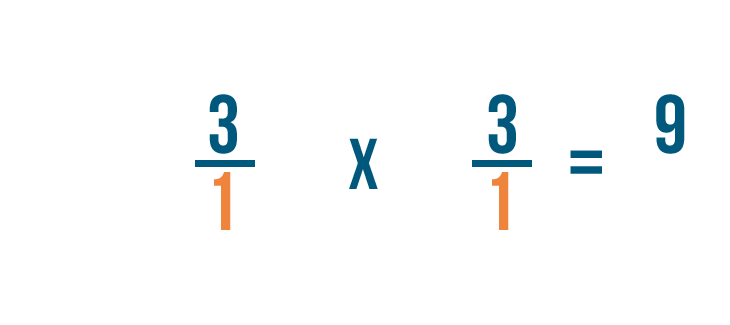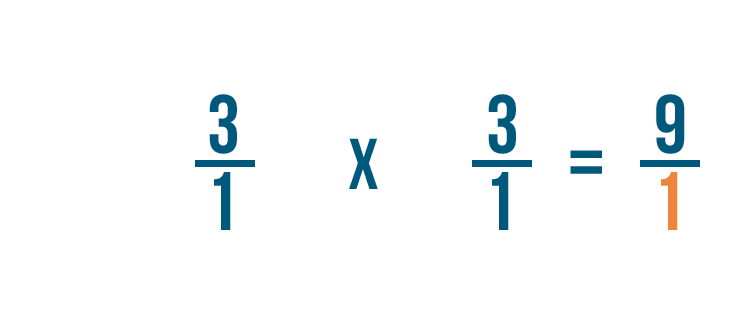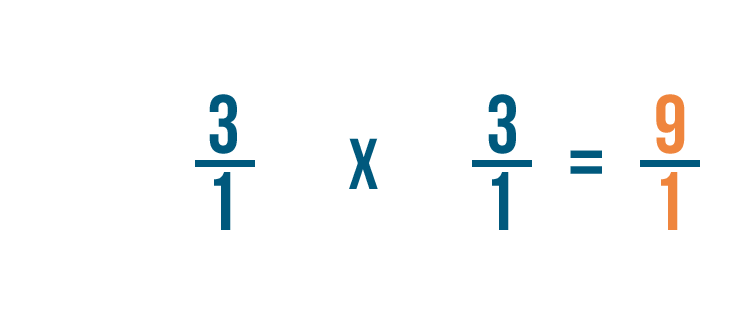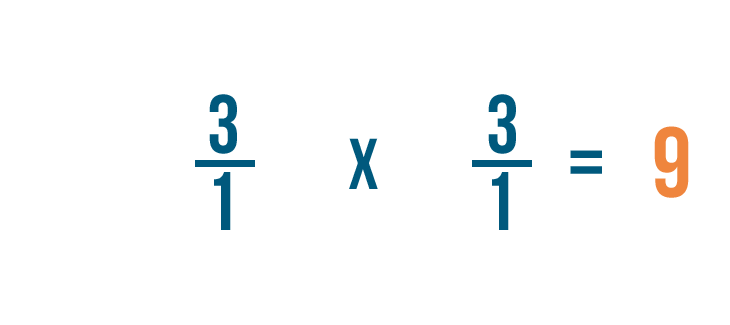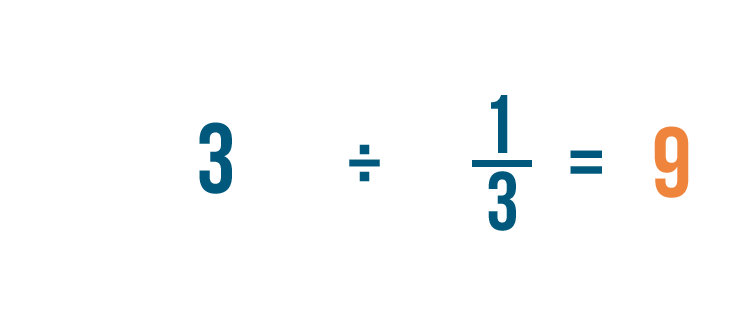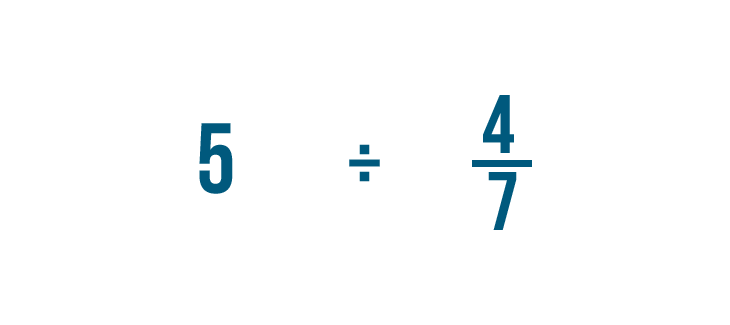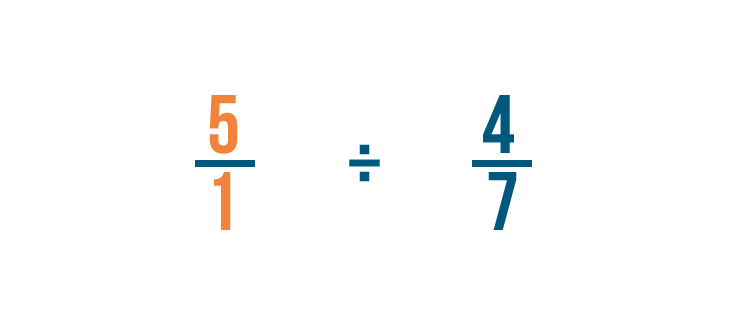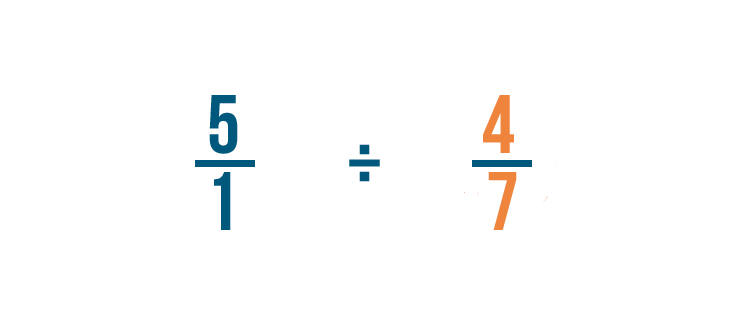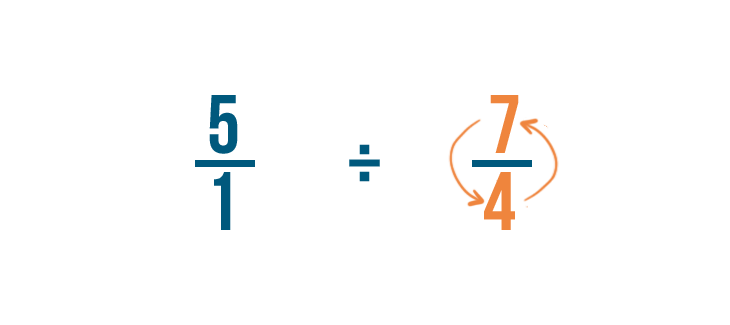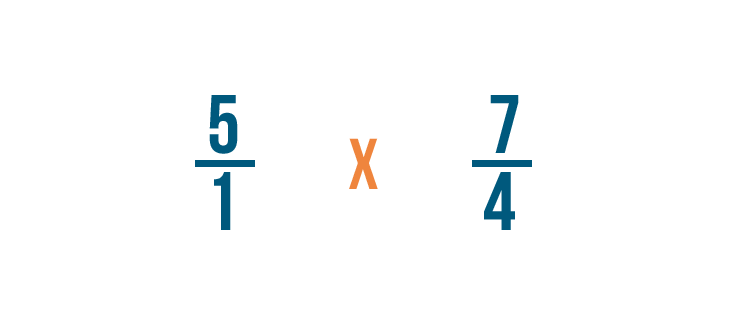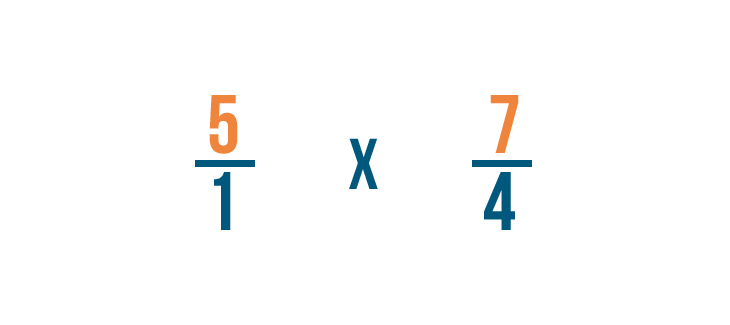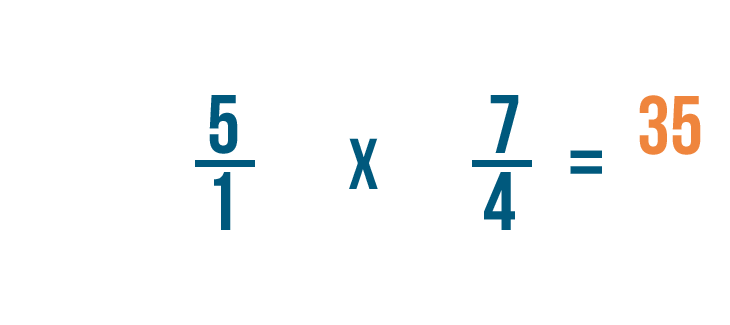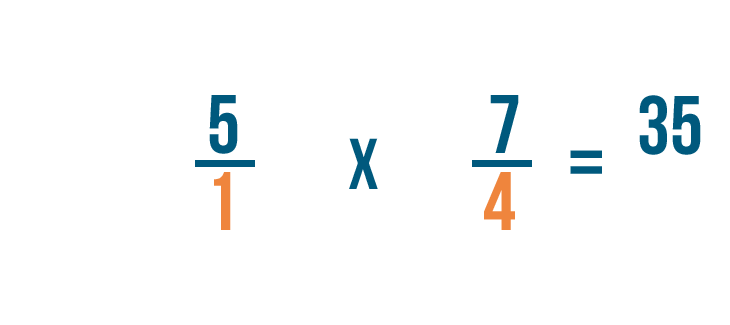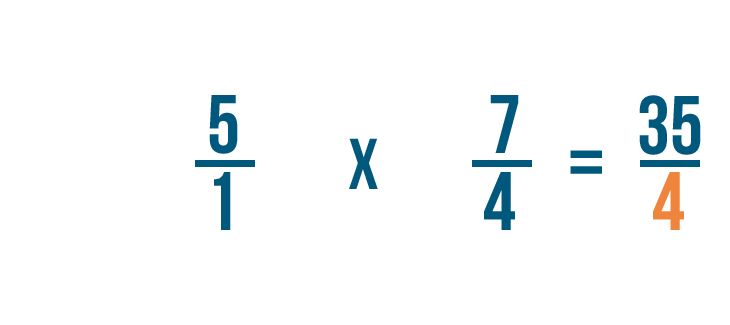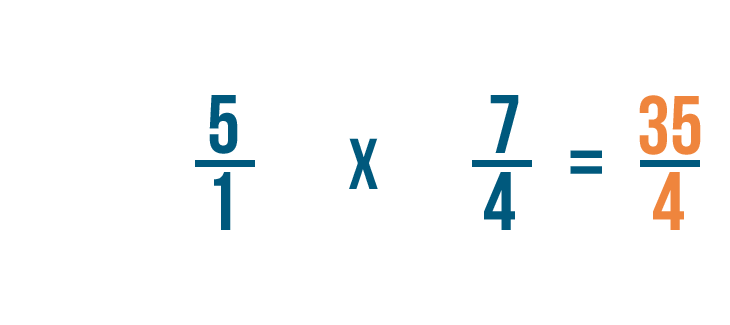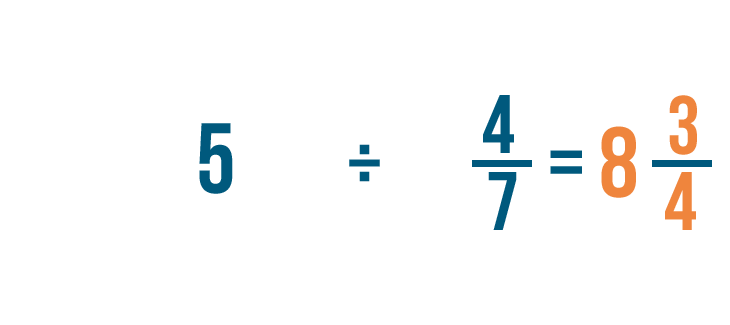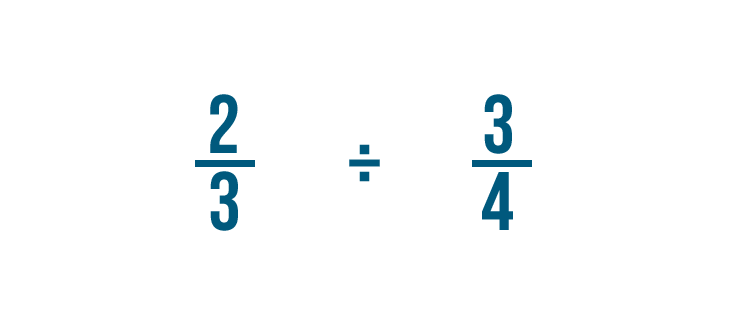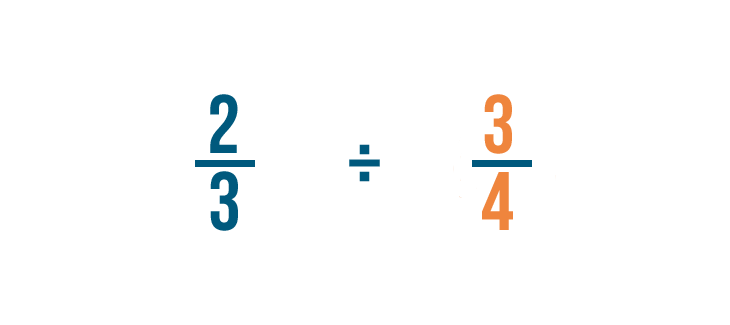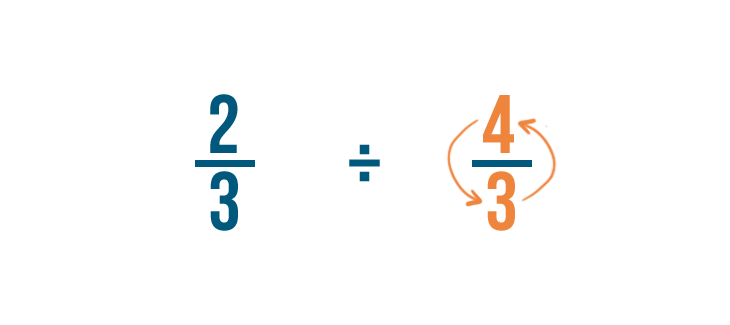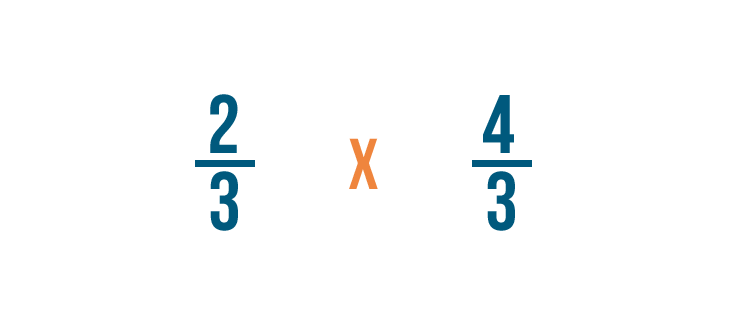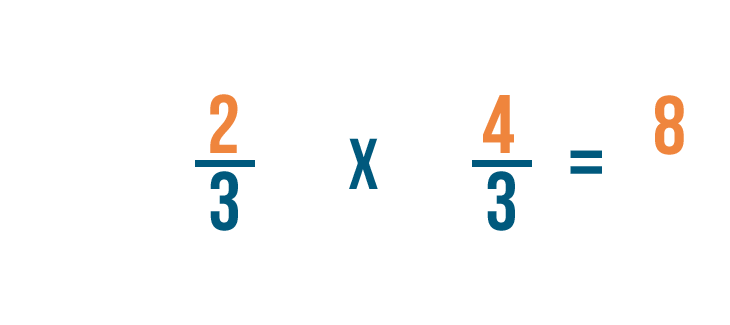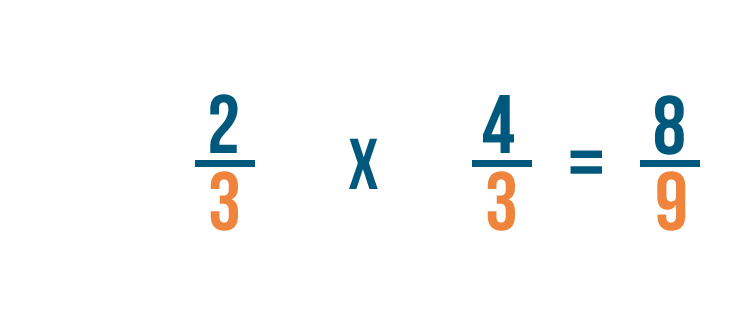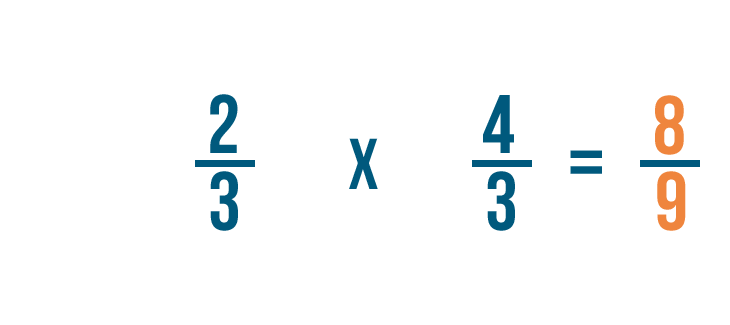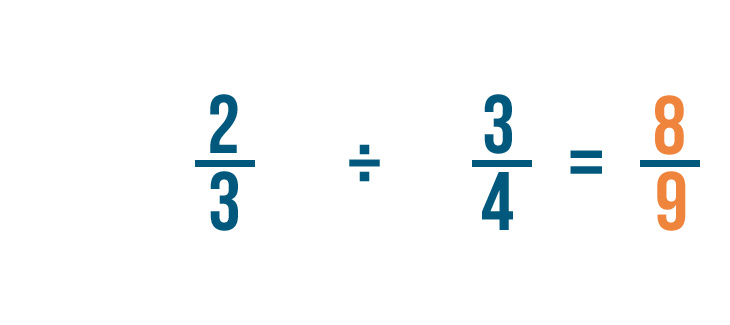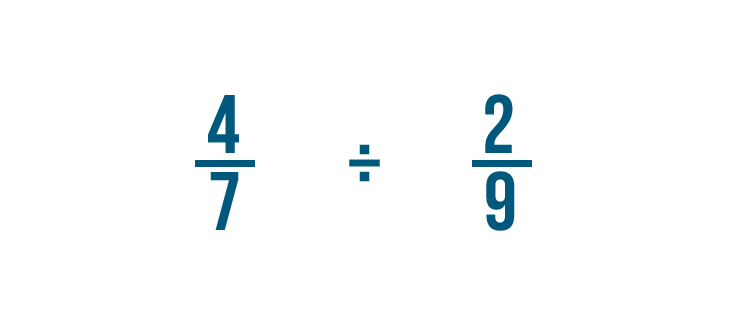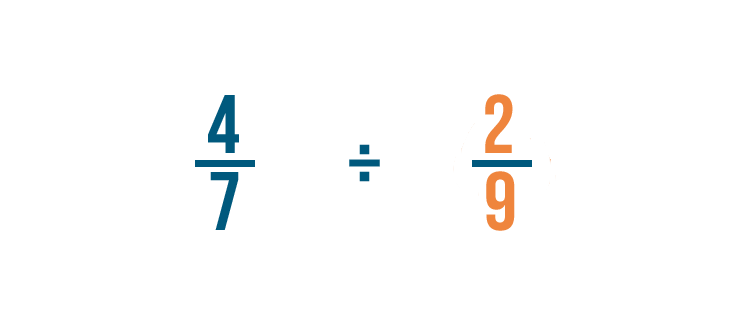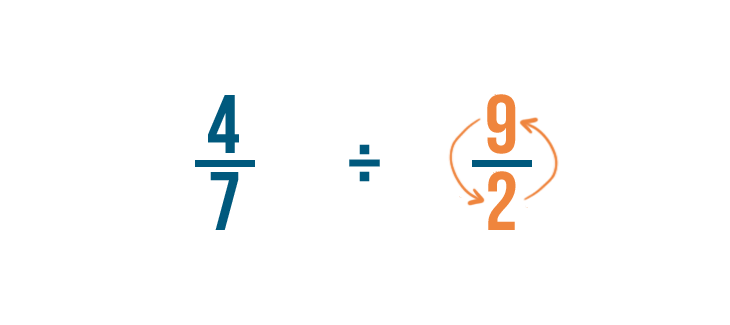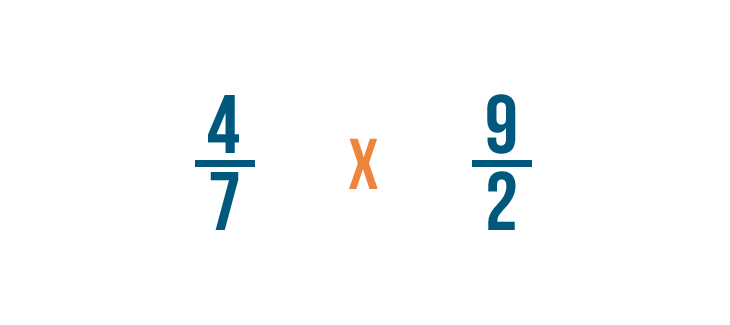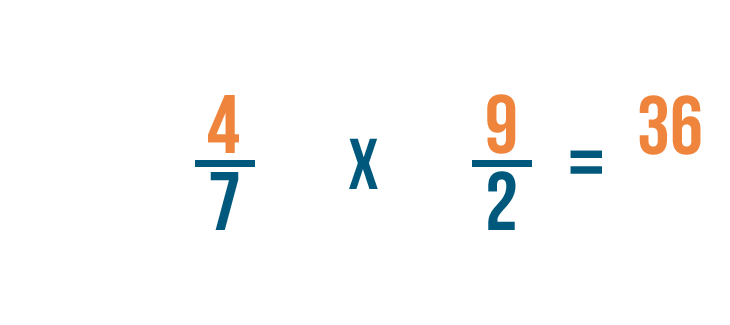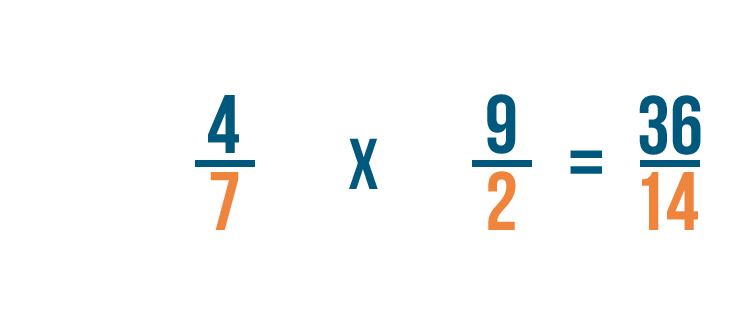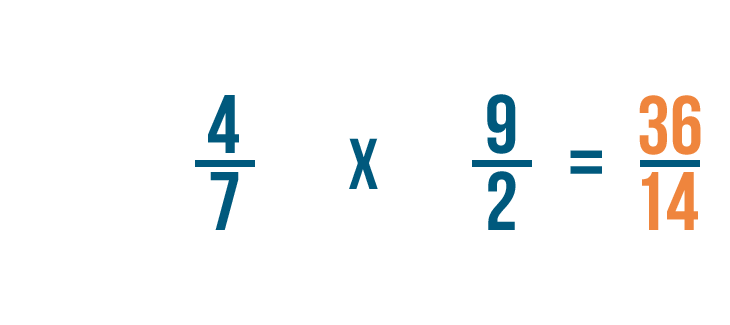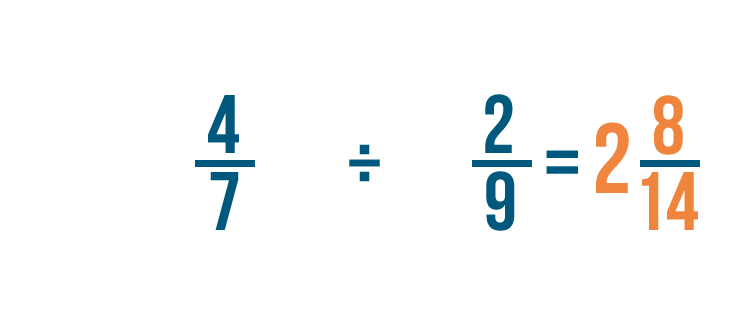Fractions

Multiplying fractions

A fraction is a part of a whole. In the last lesson, you learned how to add and subtract fractions. But that’s not the only kind of math you can do with fractions. There are times when it will be useful to multiply fractions too.

Click through the slideshow to learn how to write a multiplication problem with fractions.

• 

  Let's set up a multiplication example with fractions. Suppose you drink 2/4 of a pot of coffee every morning.

• 

  But your doctor just told you that you need to cut down your coffee drinking by half.

• 

  Now you need to figure out how much 1/2 of 2/4 of a pot of coffee is.

• 

  This may not look like a multiplication problem. But when you see the word of with fractions, it means you need to multiply.

• 

  To set up the example, we'll just replace the word of with a multiplication sign.

• 

  Now our example is ready to be solved.

• 

  Unlike regular multiplication, which gives you a larger number...

• 

  Unlike regular multiplication, which gives you a larger number...multiplying fractions will always give you a smaller number.

• 

  So when we multiply 1/2 times 2/4...

• 

  So when we multiply 1/2 times 2/4...our answer will be smaller than 2/4.

• 

  Here's another example. Let's say you have 3/5 of a cup of chocolate filling.

• 

  You want to put an equal amount of filling in each of these 4 cupcakes.

• 

  You could say that you want to put 1/4 of 3/5 of a cup of filling in each cupcake.

• 

  Just like we did before, we'll change the word of into a multiplication sign.

• 

  And now our fractions are ready to be multiplied.

• 

Now it's your turn! Try setting up the multiplication problem below. Don't worry about solving it yet!

A recipe calls for 2/3 of a cup of milk. You want to cut the recipe in half.

Solving multiplication problems with fractions

Now that we know how to set up multiplication problems with fractions, let's practice solving a few. If you feel comfortable multiplying whole numbers, you're ready to multiply fractions.

Click through slideshow to learn how to multiply two fractions.

• 

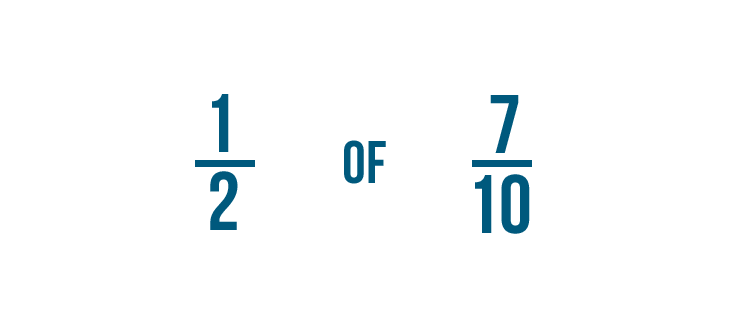
  Let's multiply to find 1/2 of 7/10.

• 

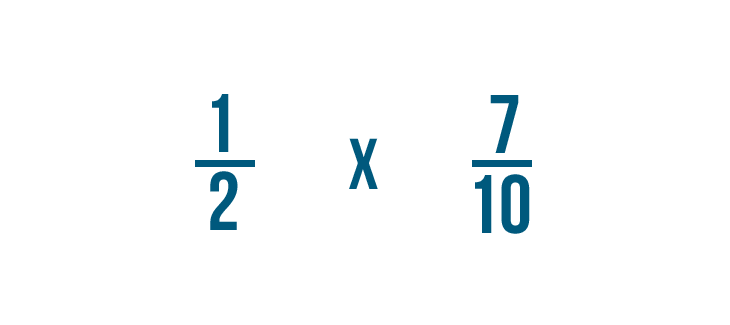
  Just like we did earlier, we'll replace the word of with a multiplication sign. Now we're ready to multiply.

• 

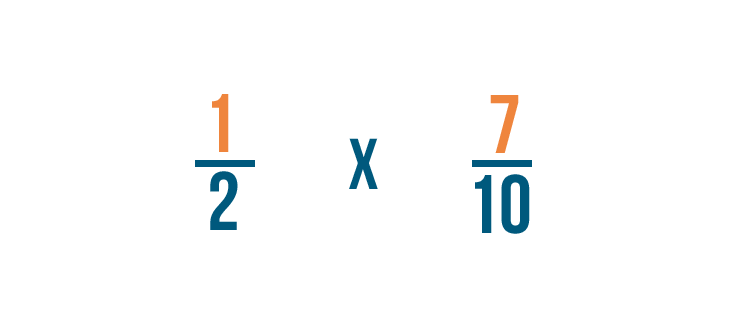
  First, we'll multiply the numerators: 1 and 7.

• 

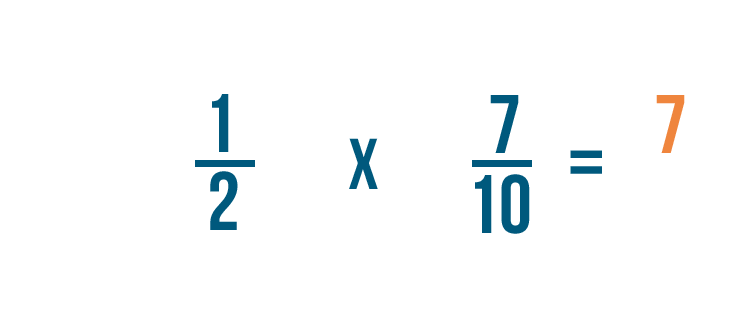
  1 times 7 equals 7, so we'll write 7 to the right of the numerators.

• 

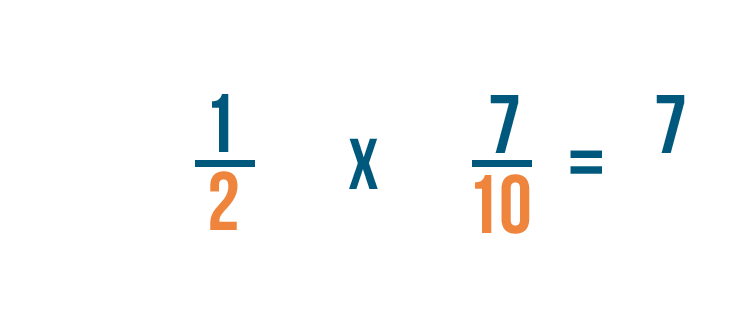
  When we added fractions, the denominators stayed the same. But when we multiply, the denominators get multiplied too.

• 

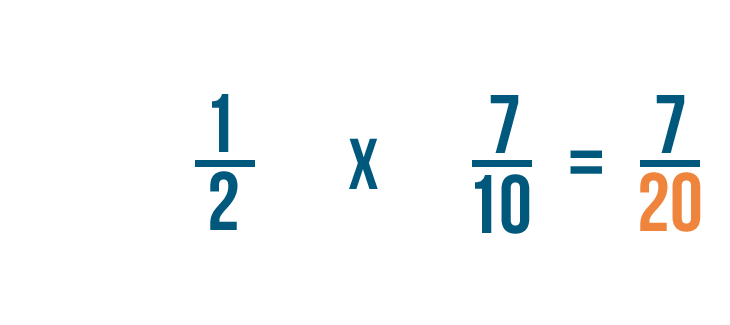
  2 times 10 equals 20, so we'll write 20 to the right of the denominators.

• 

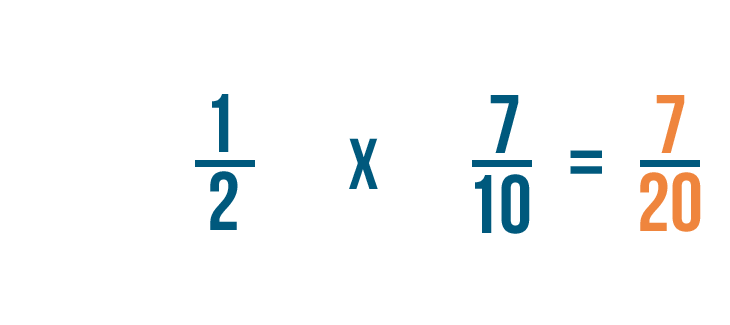
  Now we know 1/2 times 7/10 equals 7/20.

• 

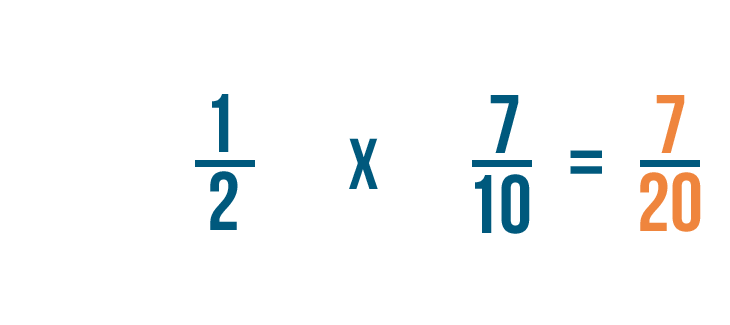
  We could also say 1/2 of 7/10 is 7/20.

• 

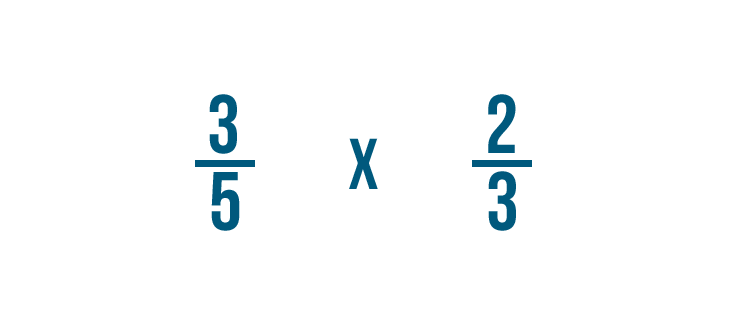
  Let's try another example: 3/5 times 2/3.

• 

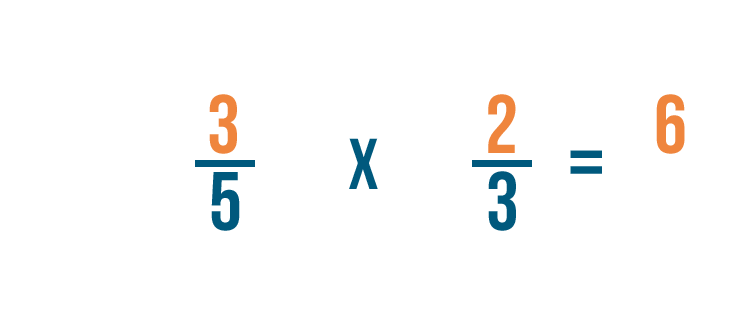
  First, we'll multiply our numerators. 3 times 2 equals 6.

• 

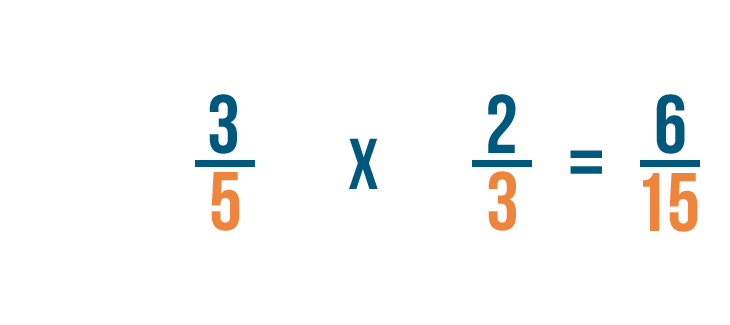
  Next, we'll multiply our denominators. 5 times 3 equals 15.

• 

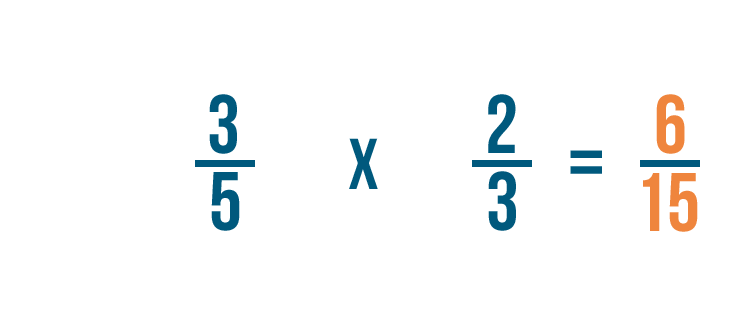
  So 3/5 times 2/3 equals 6/15.

• 

Now you try it! Try solving the multiplication problems below. Don't worry about reducing the answer for now.

Multiplying a fraction and a whole number

Multiplying a fraction and a whole number is similar to multiplying two fractions. There's just one extra step: Before you can multiply, you'll need to turn the whole number into a fraction. This slideshow will show you how to do it.

Click through the slideshow to learn how to multiply a fraction and a whole number.

• 

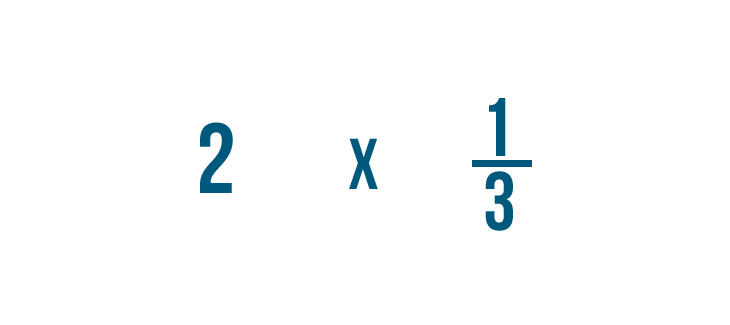
  Let's multiply 2 times 1/3. Remember, this is just another way of asking, "What's 1/3 of 2?"

   

• 

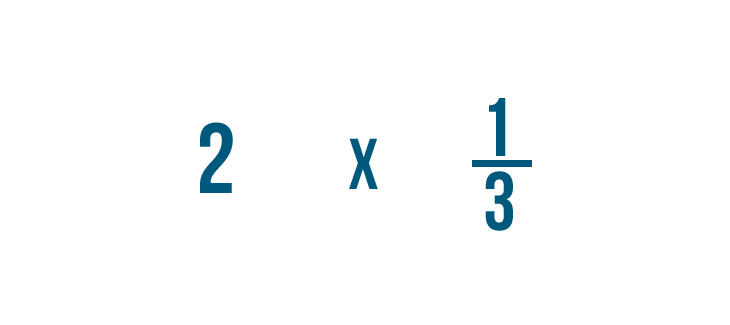
  Before we start, we need to make sure these numbers are ready to be multiplied.

• 

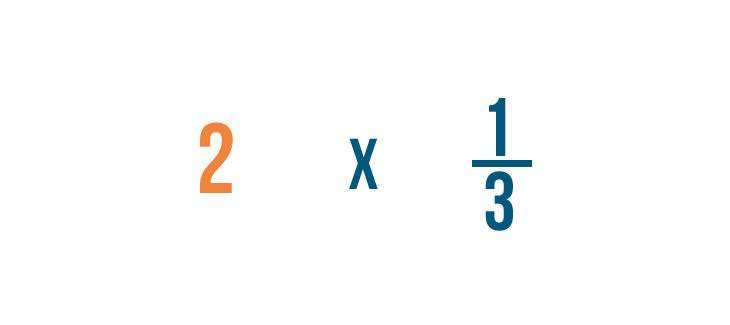
  We can't multiply a whole number and a fraction, so we're going to have to write 2 as a fraction.

• 

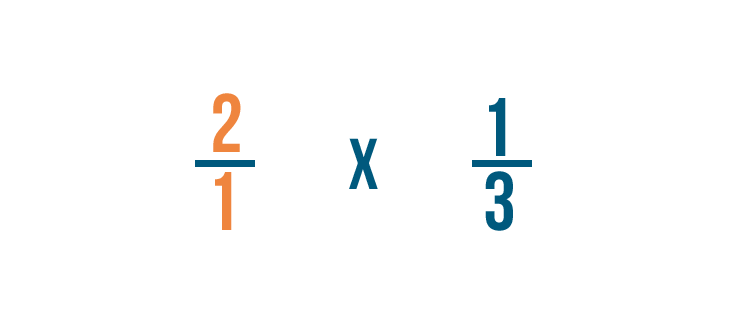
  As you learned in Introduction to Fractions, we can also write 2 as 2/1.That's because 2 can be divided by 1 twice.

• 

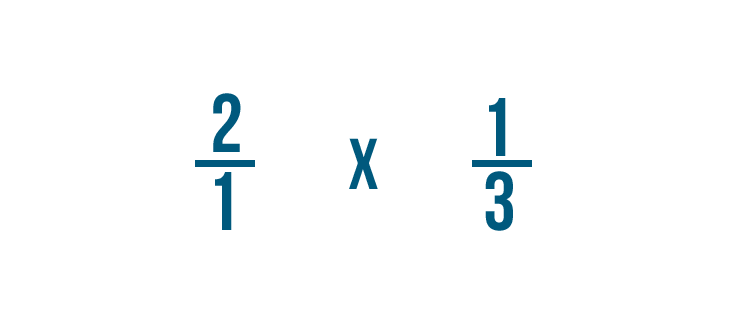
  Now we're ready to multiply!

• 

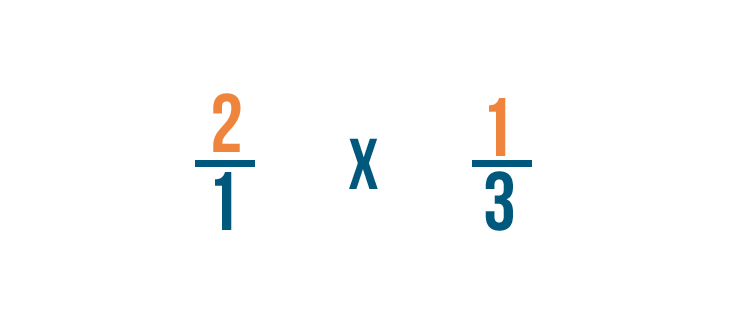
  First, we'll multiply the numerators: 2 and 1.

• 

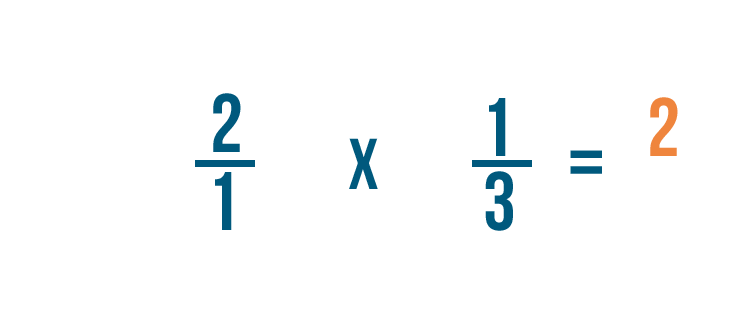
  2 times 1 equals 2. We'll line the 2 up with the numerators.

• 

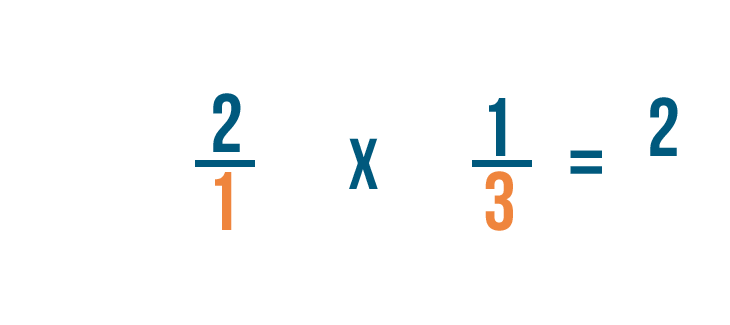
  Next, we'll multiply the denominators: 1 and 3.

• 

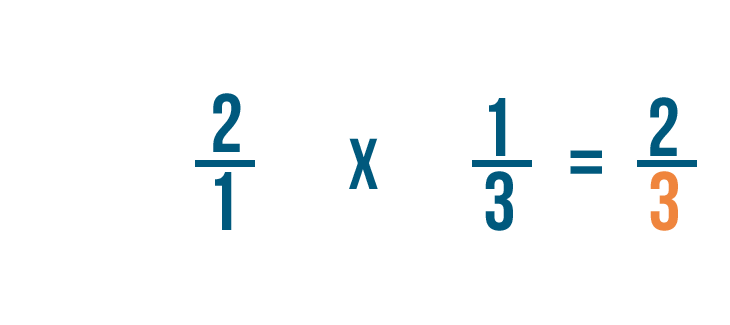
  1 times 3 equals 3. We'll line the 3 up with the denominators.

• 

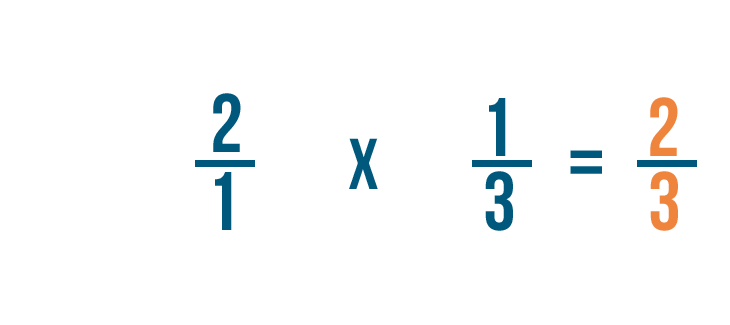
  So 2/1 times 1/3 equals 2/3. We could also say 1/3 of 2 is 2/3.

• 

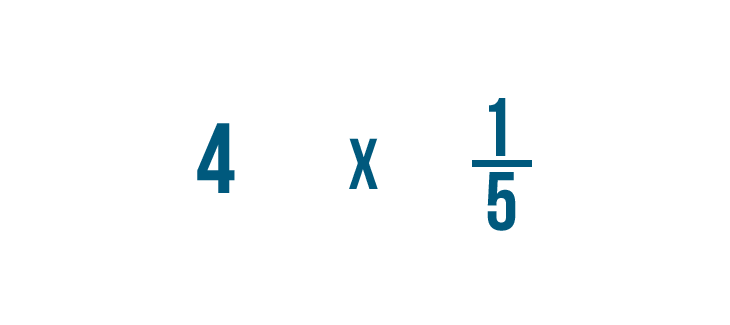
  Let's try another example: 4 times 1/5.

• 

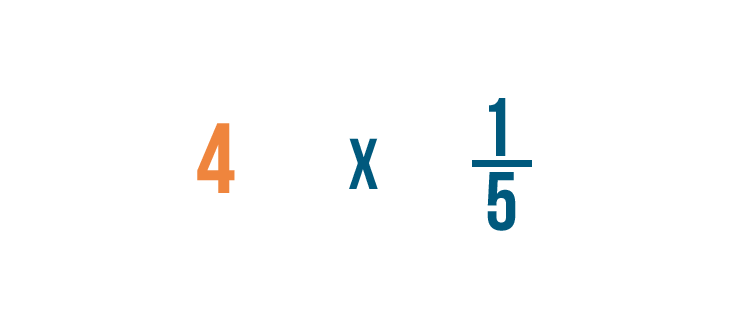
  We'll have to write 4 as a fraction before we start.

• 

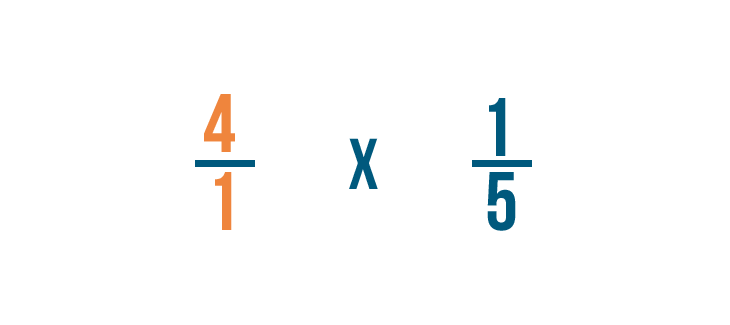
  We'll rewrite 4 as 4/1. Now we're ready to multiply.

• 

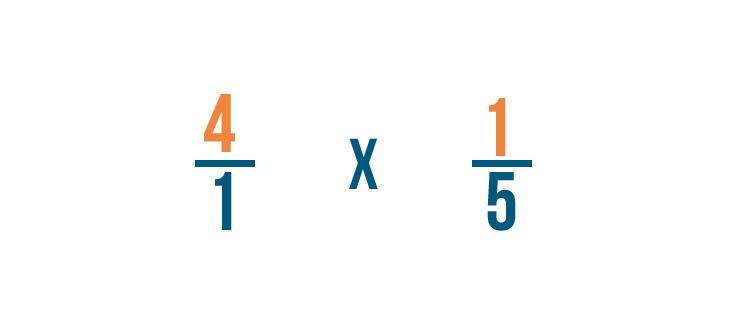
  First, we'll multiply the numerators: 4 and 1.

• 

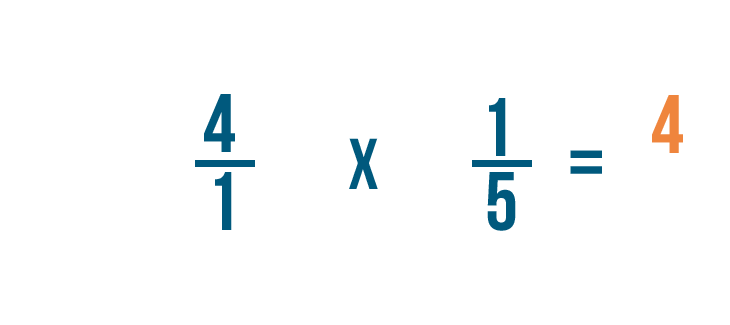
  4 times 1 equals 4, so the numerator of our answer is 4.

• 

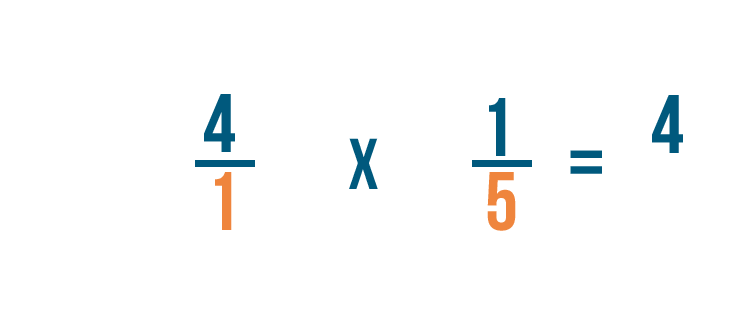
  Next, we'll multiply the denominators: 1 and 5.

• 

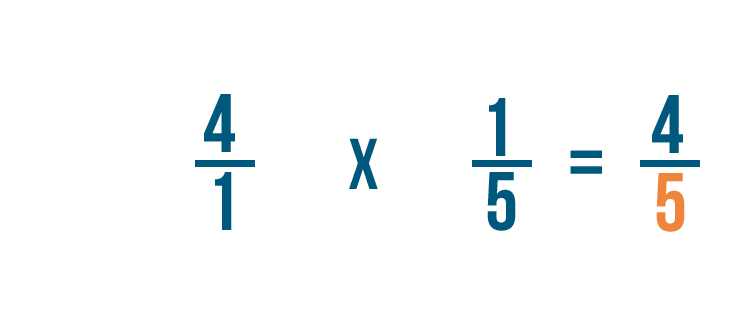
  1 times 5 equals 5, so 5 is the denominator of our answer.

• 

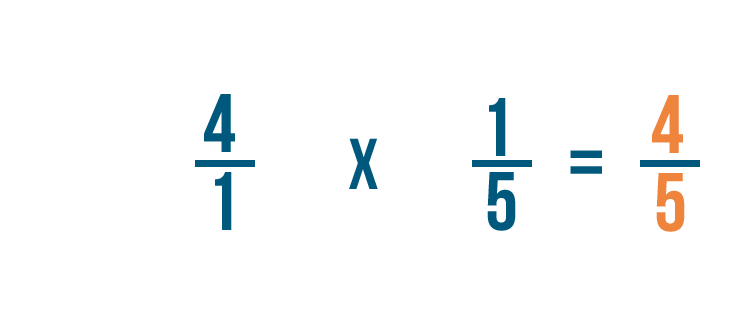
  So 4/1 times 1/5 equals 4/5.

• 

Now you try it! Try solving the multiplication problems below. Don't worry about reducing the answer for now.

Dividing fractions

Over the last few pages, you've learned how to multiply fractions. You might have guessed that you can divide fractions too. You divide fractions to see how many parts of something are in something else. For example, if you wanted to know how many fourths of an inch are in four inches, you could divide 4 by 1/4.

Let's try another example. Imagine a recipe calls for 3 cups of flour, but your measuring cup only holds 1/3, or one-third, of a cup. How many thirds of a cup should you add?

We'll need to find out how many thirds of a cup are in three cups. In other words, we'll need to divide three by one-third.

We'd write the problem like this:

3  /  1/3

Now it's your turn! Try setting up these division problems with fractions. Don't worry about solving them yet!

A recipe calls for 3/4 of a cup of water. You only have a 1/8 measuring cup.

If you have beads that are 3/4 of an inch wide, how many can fit on a string that's 5 inches long?

Solving division problems with fractions

Now that we know how to write division problems, let's practice by solving a few. Dividing fractions is a lot like multiplying. It just requires one extra step. If you can multiply fractions, you can divide them too!

Click through the slideshow to learn how to divide a whole number by a fraction.

• 

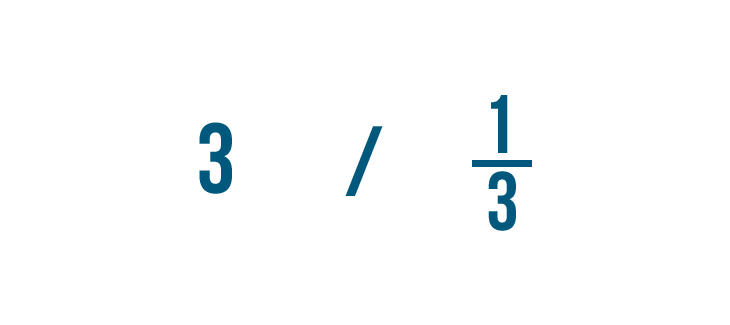
  Let's divide 3 by 1/3. Remember, this is just another way to ask, "How many thirds are in 3?"

• 

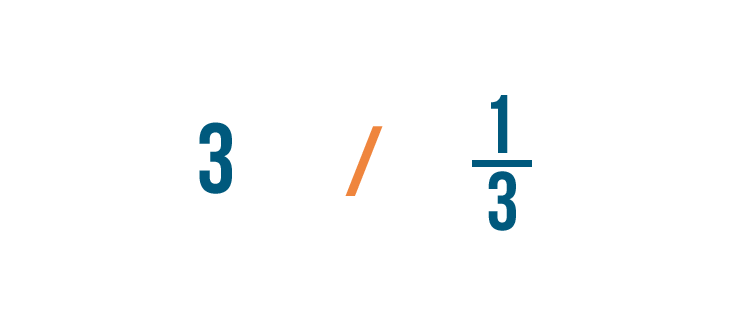
  In our lesson on division, you learned how to write the division sign like this (/).

• 

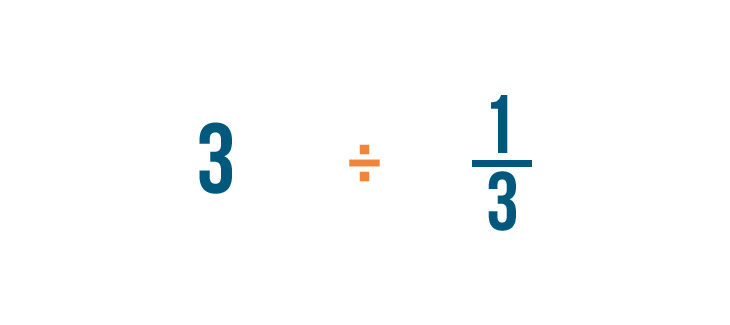
  When dividing fractions, it will help to use the other symbol for division (÷) so we don't mistake it for a fraction.

• 

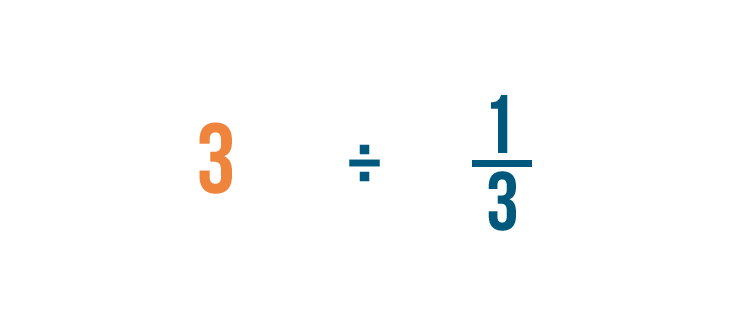
  Just like multiplication, we'll start by looking for any whole numbers in our problem. There's one: 3.

• 

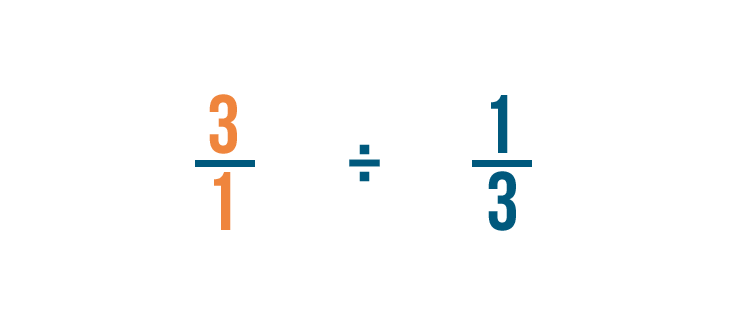
  Remember, 3 is the same thing as 3/1.

• 

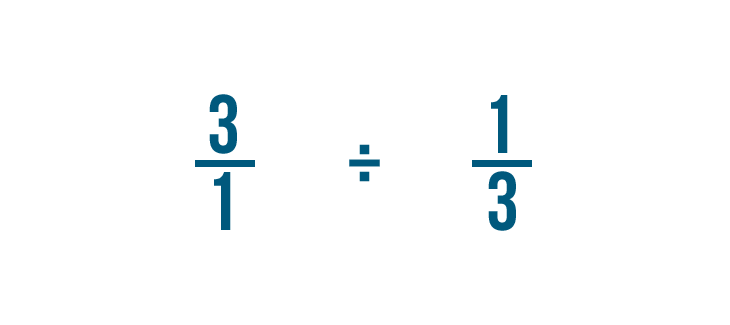
  Before we can divide, we need to make one more change.

• 

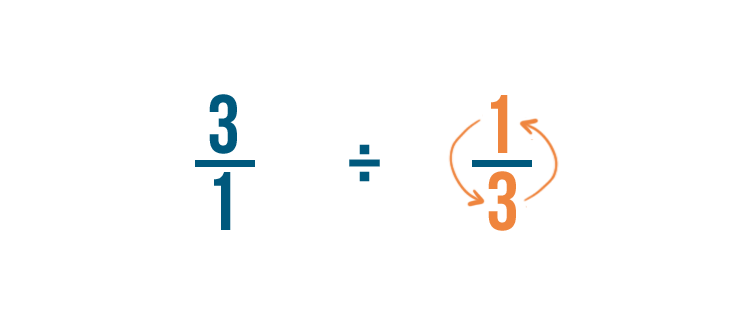
  We'll switch the numerator and the denominator of the fraction we're dividing by: 1/3 in this example.

• 

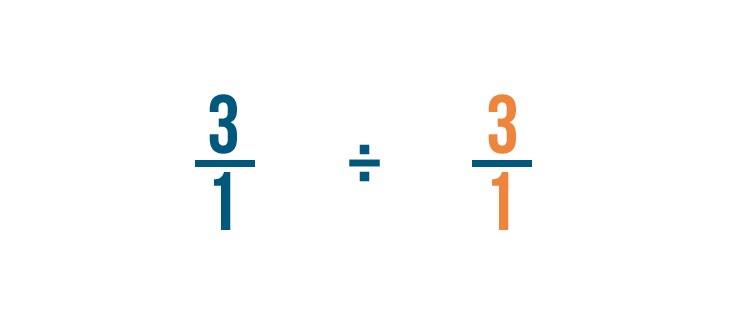
  So 1/3 becomes 3/1.

• 

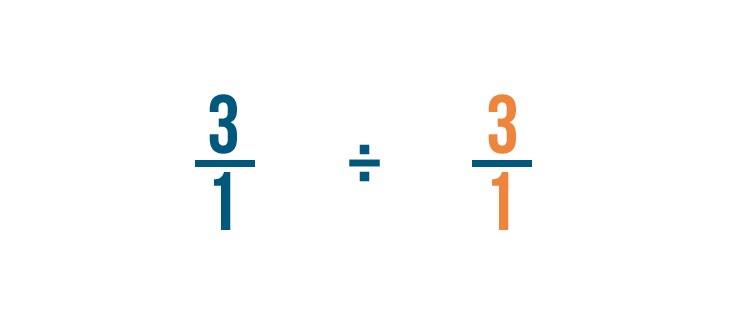
  This is called finding the reciprocal, or opposite, of the fraction.

• 

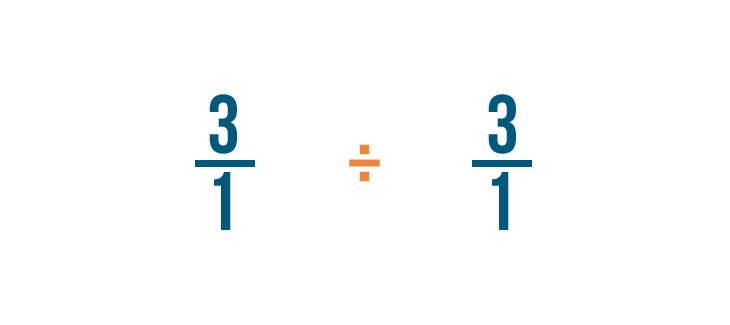
  Since we're using the opposite of our original fraction, we'll also change the division sign (÷) to a multiplication sign (x). 

• 

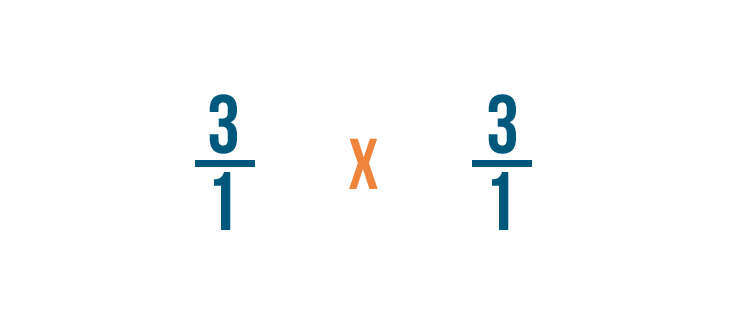
  That's because multiplication is the opposite of division. 

• 

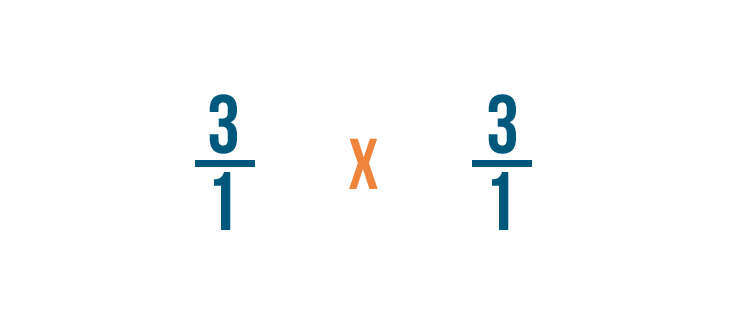
  Now we can treat this like a regular multiplication problem.

• 

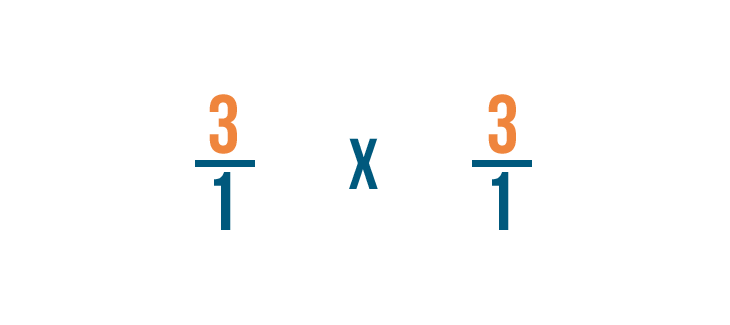
  First, we'll multiply the numerators: 3 and 3.

• 

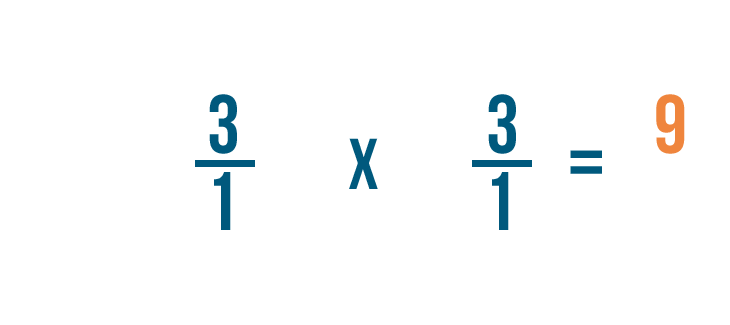
  3 times 3 equals 9, so we'll write that next to the numerators.

• 

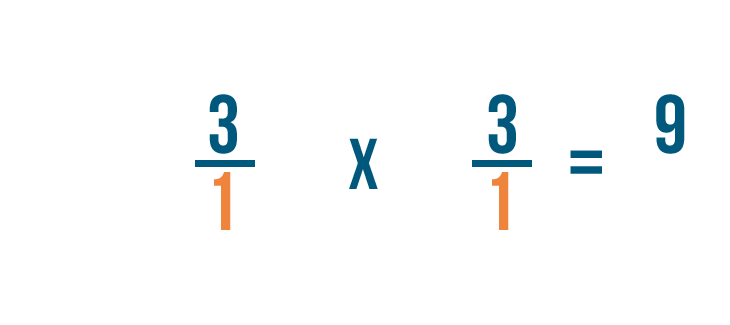
  Next, we'll multiply the denominators: 1 and 1.

• 

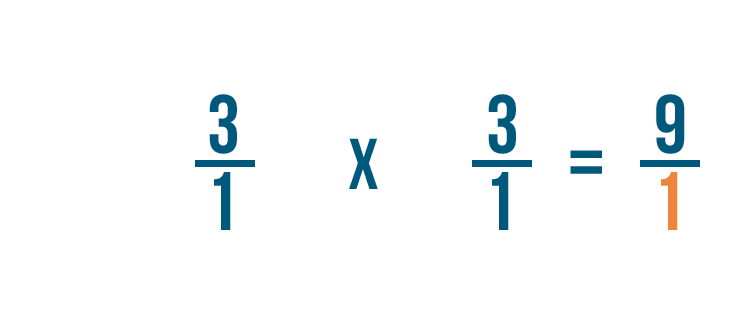
  1 times 1 equals 1, so we'll write 1 next to the denominator.
  

• 

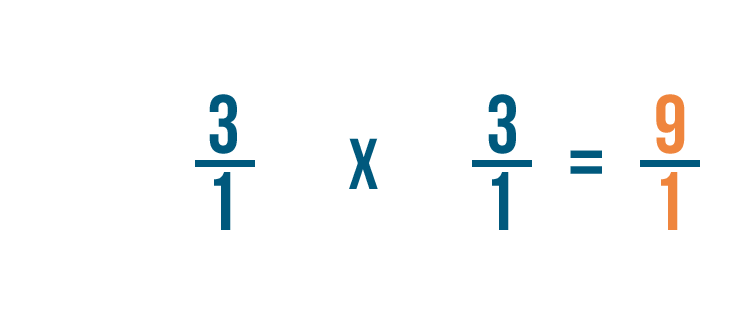
  As you can see, 3/1 x 1/3 = 9/1.

• 

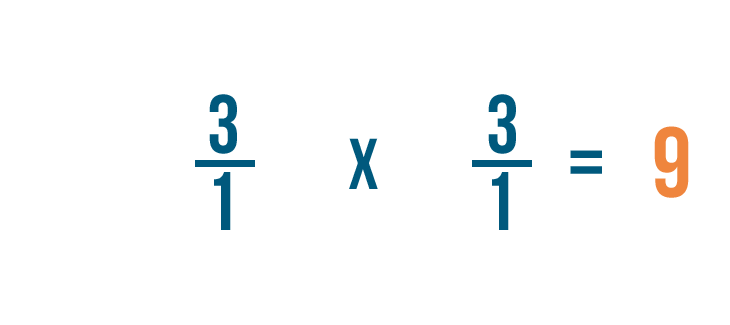
  Remember, any fraction over 1 can also be expressed as a whole number. So 9/1 = 9.

• 

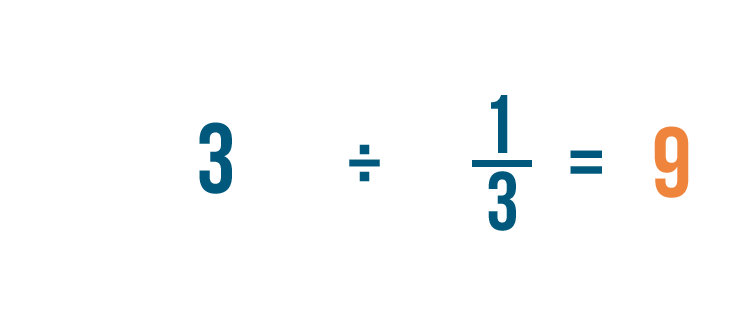
  3 ÷ 1/3 = 9. In other words, there are 9 thirds in 3.

• 

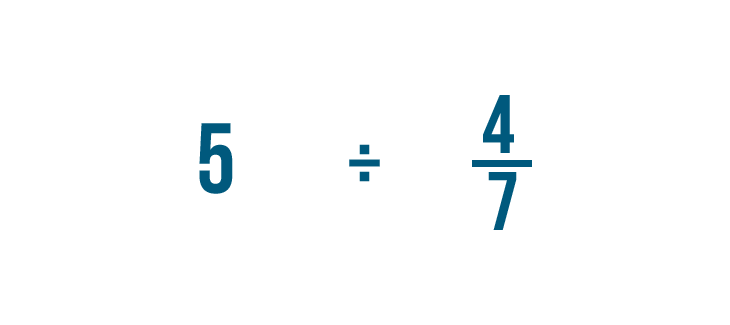
  Let's try another example: 5 divided by 4/7.

• 

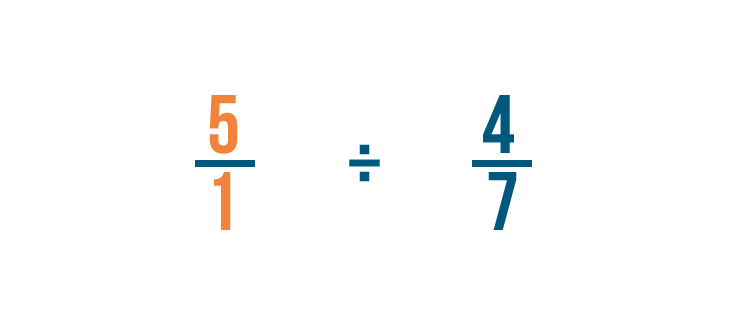
  As always, we'll rewrite any whole numbers, so 5 becomes 5/1.

• 

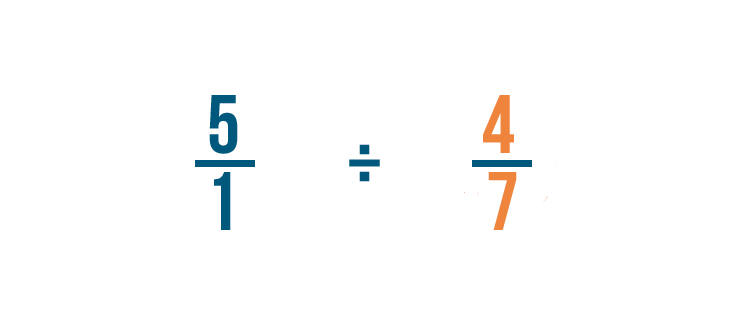
  Next, we'll find the reciprocal of 4/7. That's the fraction we're dividing by.

• 

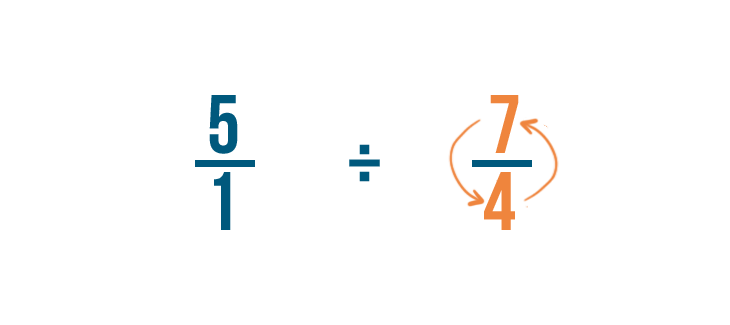
  To do that, we'll switch the numerator and denominator, so 4/7 becomes 7/4.

• 

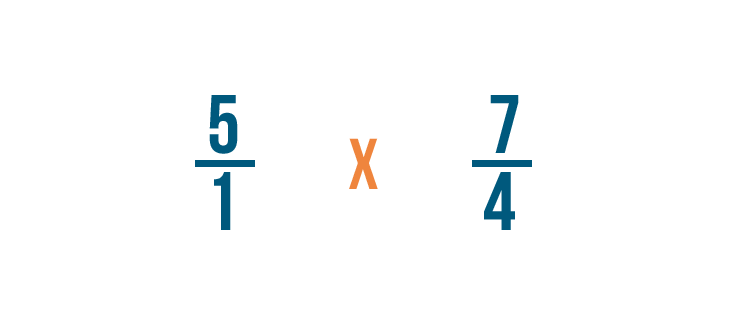
  Then we'll change the division sign (÷) to a multiplication sign (x).

• 

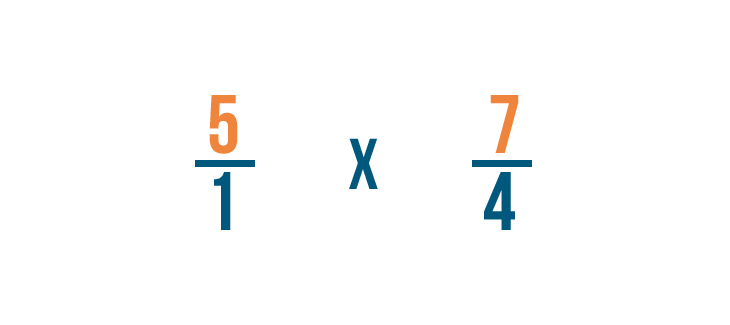
  Now we can multiply as we normally would. First, we'll multiply the numerators: 5 and 7.

• 

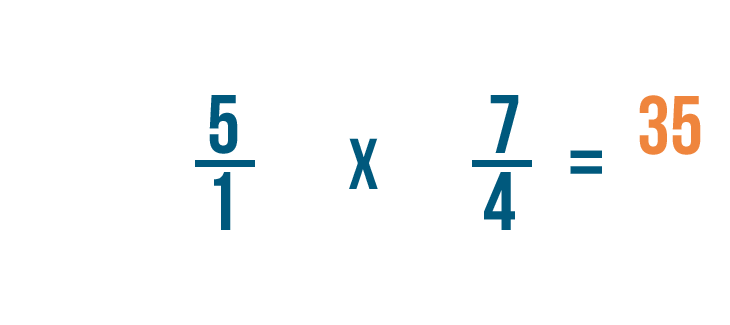
  5 times 7 equals 35, so we'll write that next to the numerators.

• 

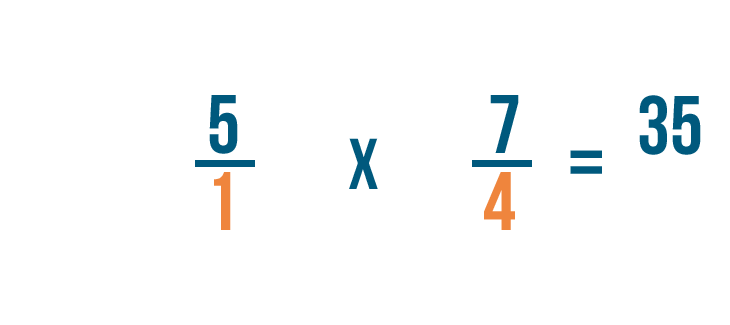
  Next, we'll multiply the denominators: 1 and 4.

• 

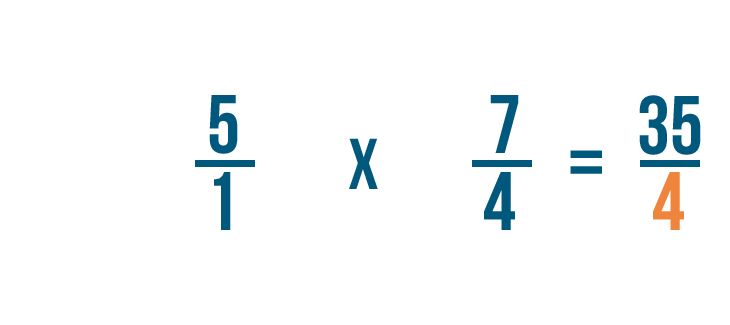
  1 times 4 equals 4, so we'll write that next to the denominators.
  

• 

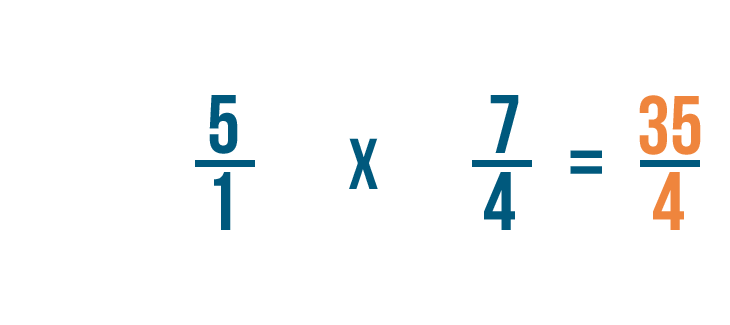
  So 5/1 x 4/7 = 35/4.
  

• 

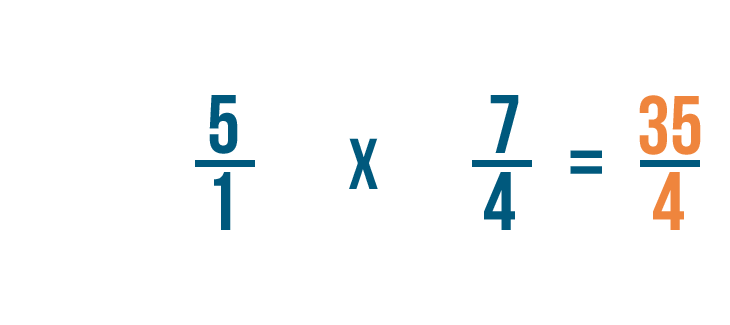
  As you learned before, we could convert our improper fraction into a mixed number to make our answer easier to read.

• 

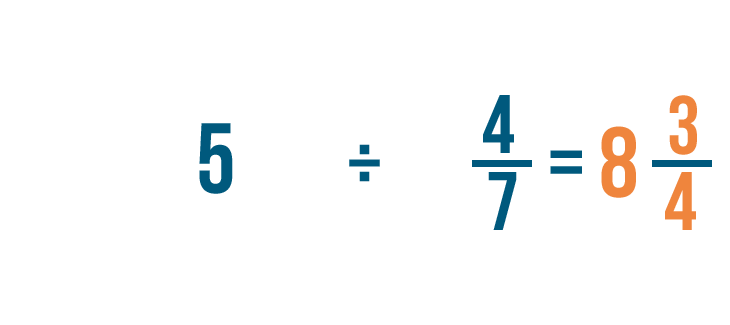
  35/4 = 8 3/4. So 5 ÷ 4/7 = 8 3/4.
  

• 

Now it's your turn! Try solving these division problems. Don't worry about reducing the answer for now.

Dividing two fractions

We just learned how to divide a whole number by a fraction. You can use the same method to divide two fractions.

Click through the slideshow to learn how to divide with two fractions.

• 

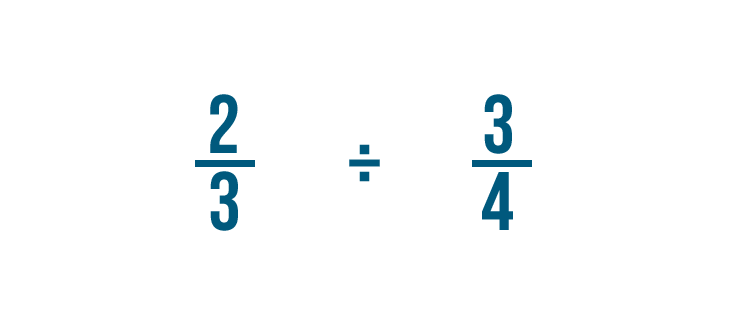
  Let's try a problem with two fractions: 2/3 ÷ 3/4. Here, we want to know how many 3/4 are in 2/3.
  

• 

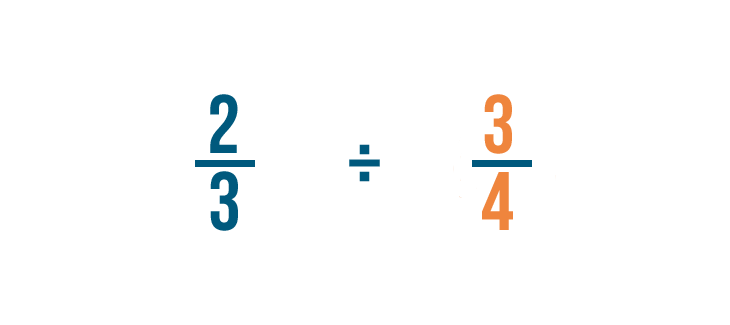
  First, we'll find the reciprocal, or opposite, of the fraction we're dividing by: 3/4.

• 

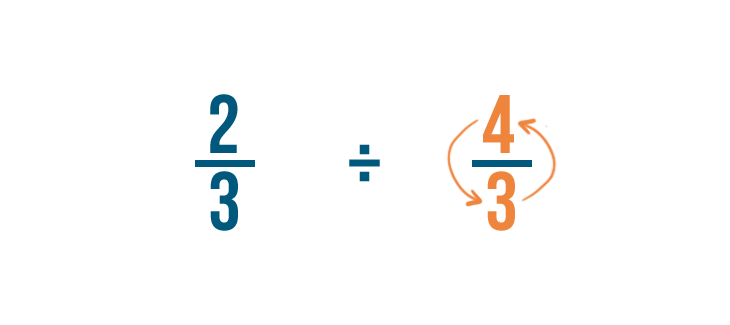
  To do that, we'll switch the numerator and denominator. So 3/4 becomes 4/3.

• 

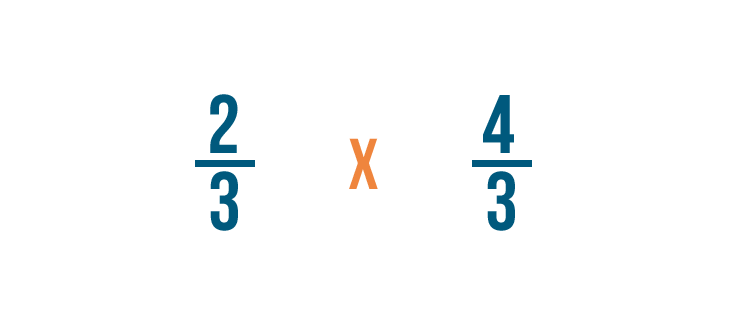
  Next, we'll change the division sign (÷) to a multiplication sign (x).

• 

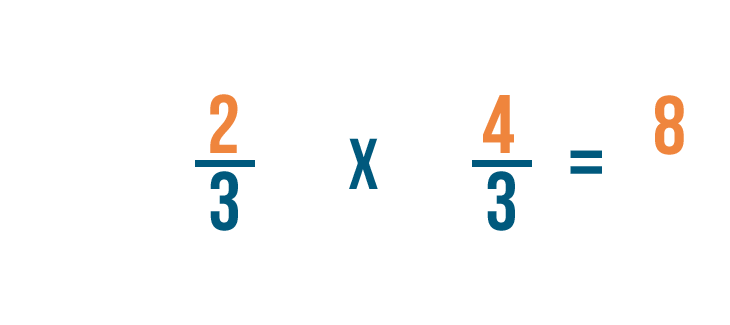
  Now we'll multiply the numerators. 2 x 4 = 8, so we'll write 8 next to the top numbers.

• 

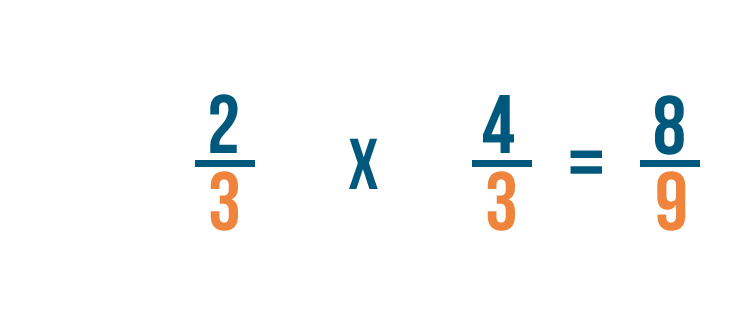
  Next, we'll multiply the denominators. 3 x 3 = 9, so we'll write 9 next to the bottom numbers.
  

• 

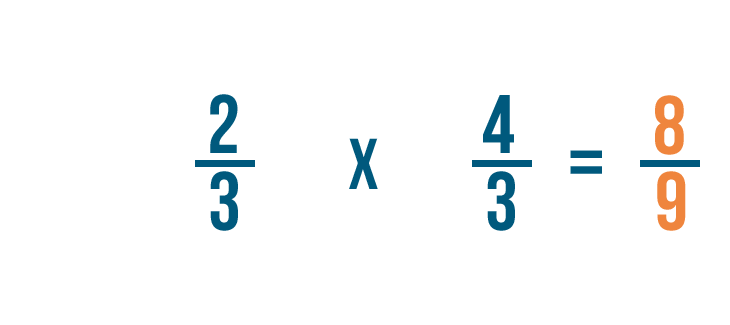
  So 2/3 x 4/3 = 8/9.
  

• 

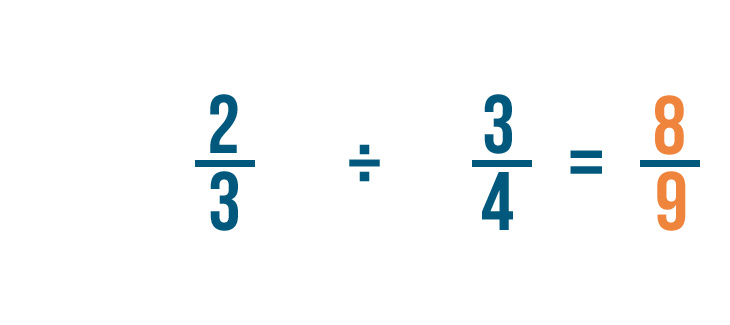
  We could also write this as 2/3 ÷ 3/4 = 8/9.
  

• 

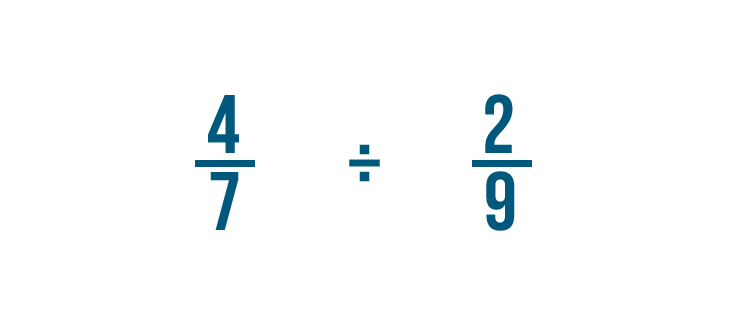
  Let's try another example: 4/7 divided by 2/9.

• 

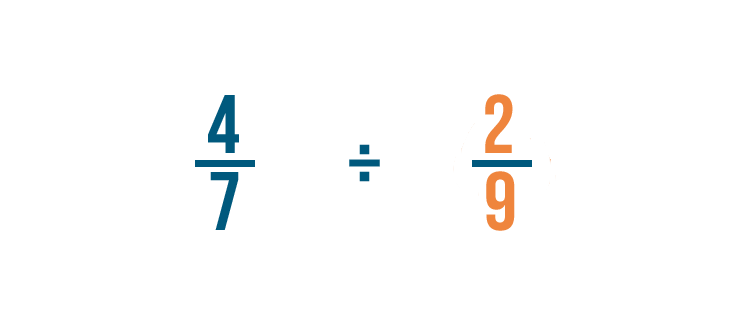
  There are no whole numbers, so we'll find the reciprocal of the fraction we're dividing by. That's 2/9.

• 

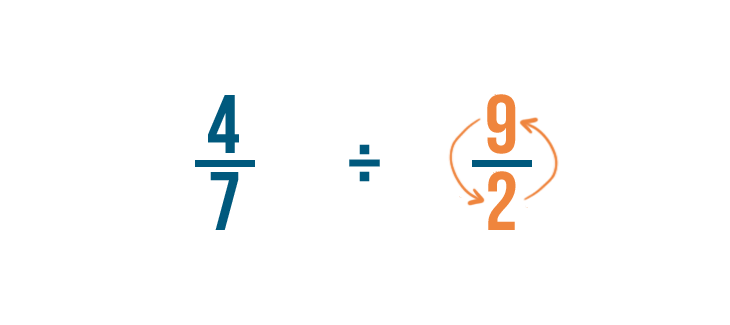
  To do that, we'll switch the numerator and denominator. So 2/9 becomes 9/2.

• 

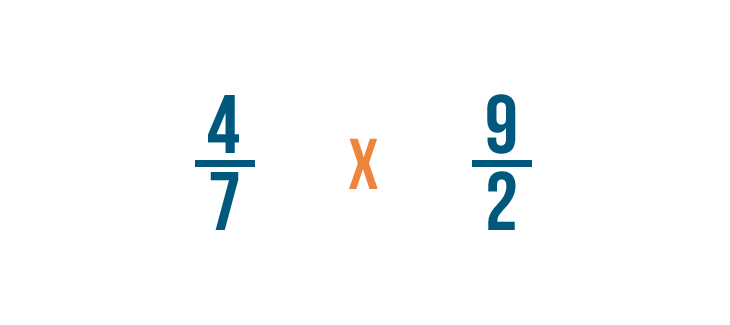
  Now we'll change the division sign (÷) to a multiplication sign (x) and multiply as normal.

• 

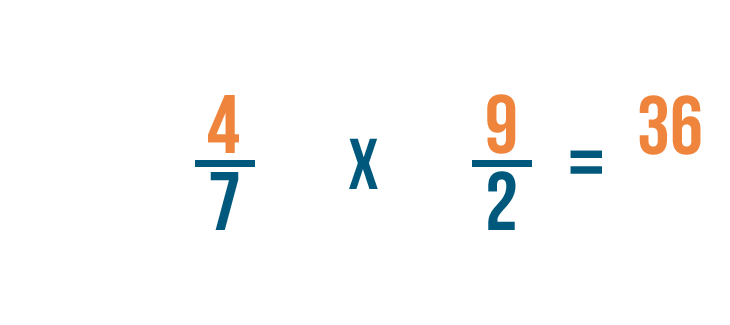
  First, we'll multiply the numerators. 4 x 9 = 36.

• 

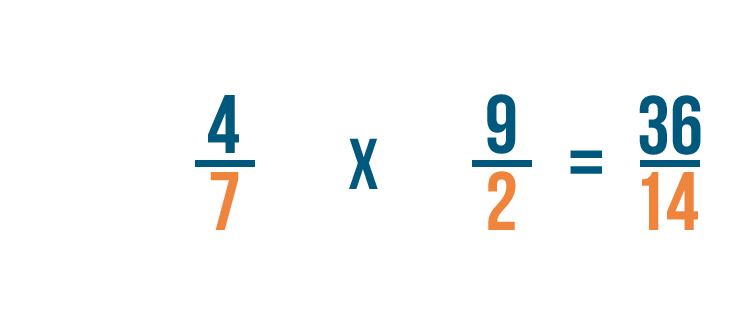
  Next, we'll multiply the denominators. 7 x 2 = 14.

• 

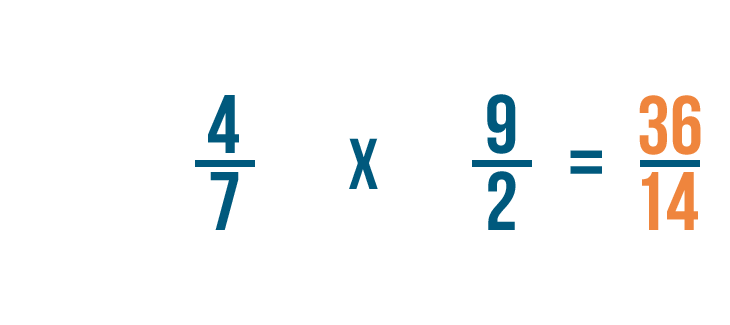
  So 4/7 x 9/2 = 36/14. Just like before, you could convert this improper fraction into a mixed number.

• 

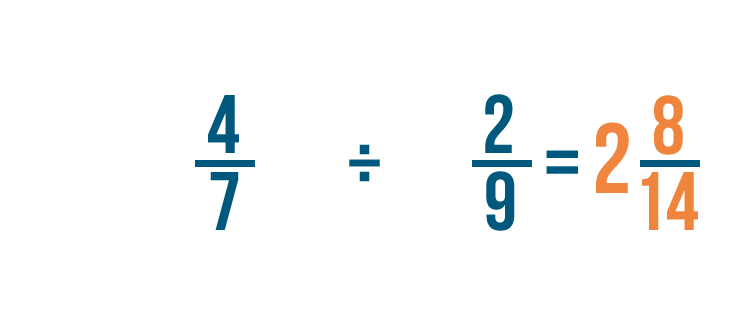
  So 4/7 ÷ 2/9 = 2 8/14.

• 

 Now you try it! Try solving these division problems. Don't worry about reducing the answer for now.

Multiplying and dividing mixed numbers

How would you solve a problem like this?

As you learned in the previous lesson, whenever you're solving a problem with a mixed number you'll need to convert it into an improper fraction first. Then you can multiply or divide as usual.

Using canceling to simplify problems

Sometimes you might have to solve problems like this:

Both of these fractions include large numbers. You could multiply these fractions the same way as any other fractions. However, large numbers like this can be difficult to understand. Can you picture 75/12, or seventy five twelfths, in your head?

  20/50  x  75/12  =  1500/600 

Even the answer looks complicated. It's 1500/600, or fifteen hundred six-hundredths. What a mouthful!

If you don't like working with large numbers, you can simplify a problem like this by using a method called canceling. When you cancel the fractions in a problem, you're reducing them both at the same time.

Canceling may seem complicated at first, but we'll show you how to do it step by step. Let's take another look at the example we just saw.

Step 1 

First, look for a numerator and a denominator that can be divided by the same number. The numerator and denominator can't be from the same fraction. This means we can't choose 20 and 50 from the problem on the left, even though they both could be divided by 10. 

In our example, it looks like both 50 and 75 can be divided by 25. We can use these numbers because they're not from the same fraction.

Step 2

Next, we'll divide 50 and 75 by 25. First, we'll divide our bottom number on the left: 50.

50 / 25 = 2

Then we'll divide the top number on the right: 75.

75 / 25 = 3

We'll write the answers to each problem next to the numbers we divided. Since 50/25 equals 2, we'll write 2 where the 50 was. 75 / 25 equals 3, so we'll write 3 where the 75 was. We can cross out, or cancel, the numbers we started with.

Our problem looks a lot simpler now, doesn't it?

Step 3

Now that we've canceled the original fractions, we can multiply our new fractions like we normally would. As always, multiply the numerators first:

20 x 3 = 60

Then multiply the denominators:

2 x 12 = 24

So 20/2  x  3/12  =  60/24, or sixty twenty-fourths.

Step 4

Finally, let's double check our work. 1500/600 would have been our answer if we had solved the problem without canceling. If we divide both 1500 and 600 by 25, we can see that 1500/600 is equal to 60/24.

We could also say that we're reducing 1500/600 to 60/24. Remember, canceling is just another way of reducing fractions before solving a problem. You'll get the same answer, no matter when you reduce them.