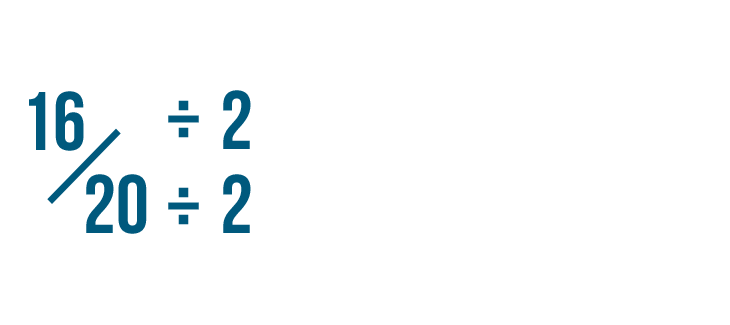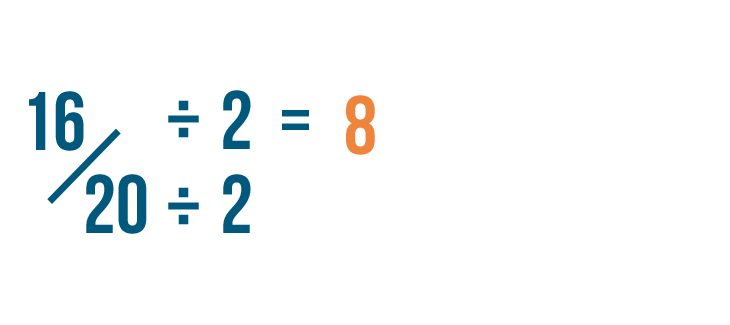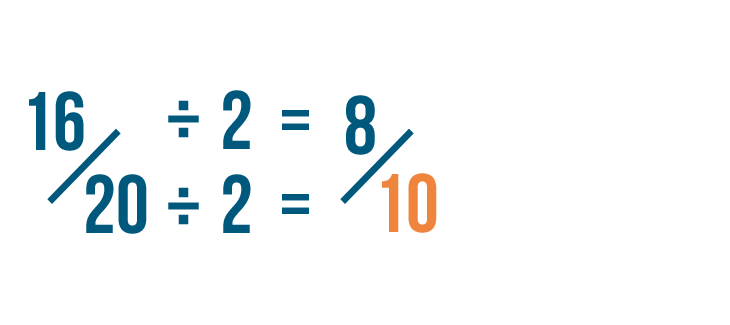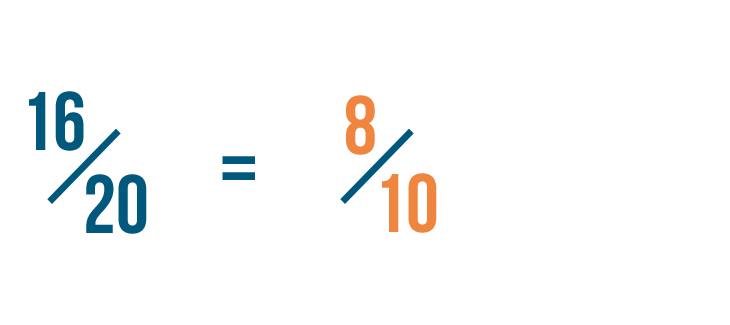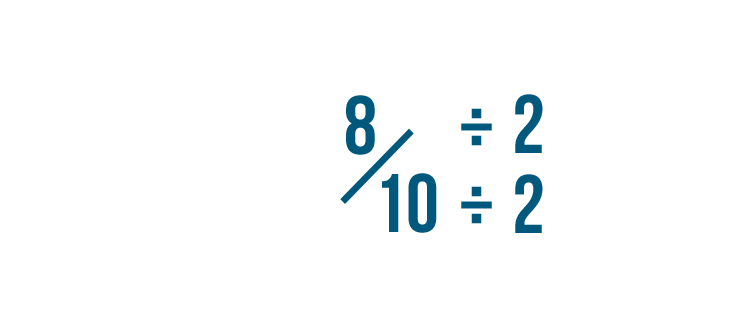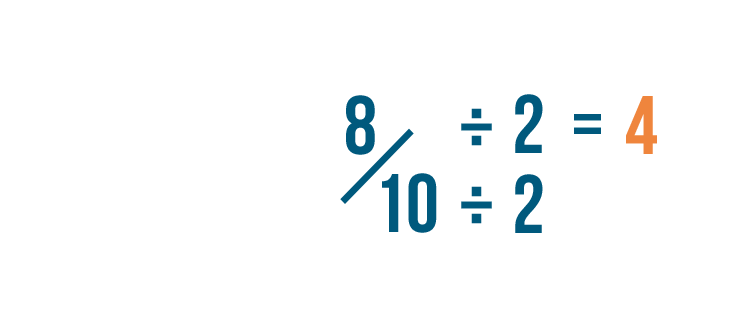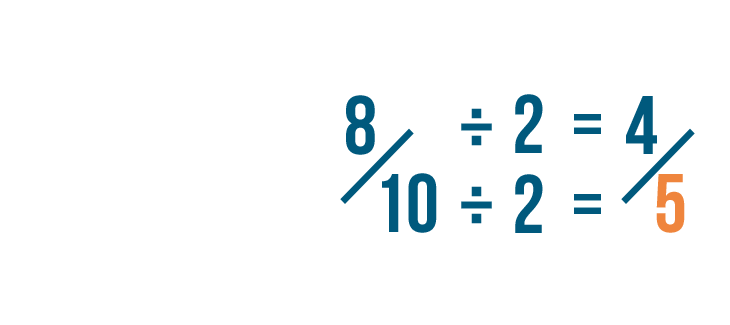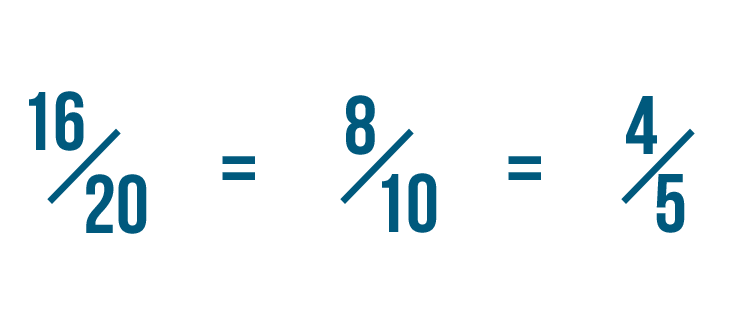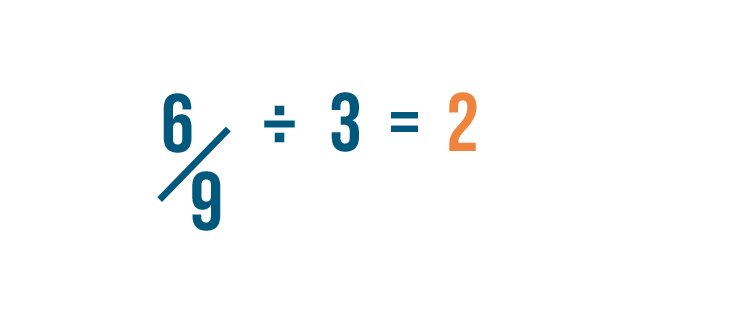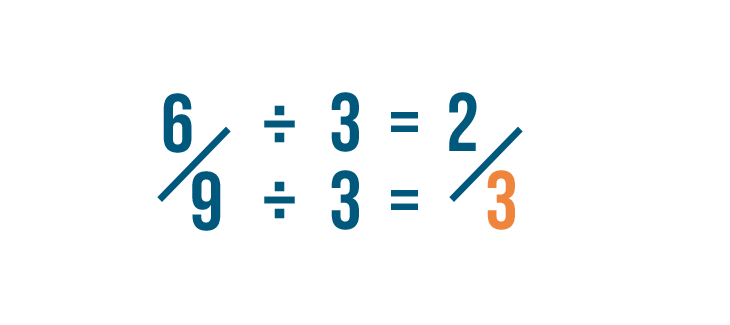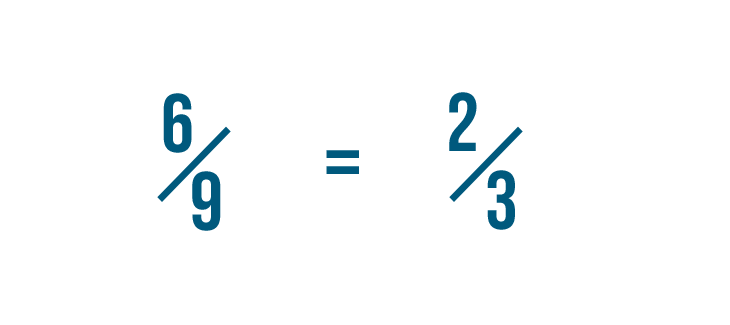Fractions

Reducing fractions

Which of these is larger: 4/8 or 1/2?

If you did the math or even just looked at the picture, you might have been able to tell that they're equal. In other words, 4/8 and 1/2 mean the same thing, even though they're written differently.

If 4/8 means the same thing as 1/2, why not just call it that? One-half is easier to say than four-eighths, and for most people it's also easier to understand. After all, when you eat out with a friend, you split the bill in half, not in eighths.

If you write 4/8 as 1/2, you're reducing it. When we reduce a fraction, we're writing it in a simpler form. Reduced fractions are always equal to the original fraction.

We already reduced 4/8 to 1/2. If you look at the examples below, you can see that other numbers can be reduced to 1/2 as well. These fractions are all equal.

5/10  = 1/2

11/22 = 1/2

36/72 = 1/2

These fractions have all been reduced to a simpler form as well.

4/12  = 1/3

14/21 = 2/3

35/50 = 7/10

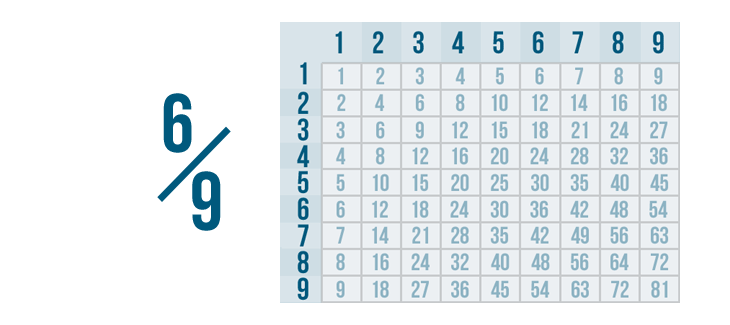
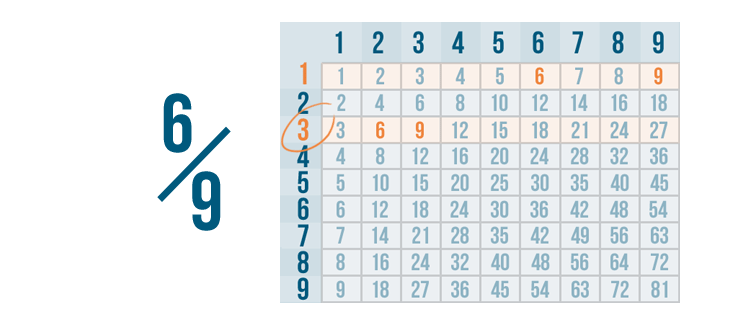
Click through the slideshow to learn how to reduce fractions by dividing.

• 

  Let's try reducing this fraction: 16/20.

• 

  Since the numerator and denominator are even numbers, you can divide them by 2 to reduce the fraction.

• 

  First, we'll divide the numerator by 2. 16 divided by 2 is 8.

• 

  Next, we'll divide the denominator by 2. 20 divided by 2 is 10.

• 

  We've reduced 16/20 to 8/10. We could also say that 16/20 is equal to 8/10.

• 

  If the numerator and denominator can still be divided by 2, we can continue reducing the fraction.

• 

  8 divided by 2 is 4.

• 

  10 divided by 2 is 5.

• 

  Since there's no number that 4 and 5 can be divided by, we can't reduce 4/5 any further.

• 

  This means 4/5 is the simplest form of 16/20.

• 

  Let's try reducing another fraction: 6/9.

• 

  As you may have noticed, the numerator and denominator are both odd numbers, so we can't divide by 2.

• 

  Instead, we'll need to find a number that 6 and 9 can be divided by. A multiplication table will make that number easy to find.

• 

  Let's find 6 and 9 on the same row. As you can see, 6 and 9 can both be divided by 1 and 3.

• 

  Dividing by 1 won't change these fractions, so we'll use the largest number that 6 and 9 can be divided by.

• 

  That's 3. This is called the greatest common divisor, or GCD. (You can also call it the greatest common factor, or GCF.)

• 

  3 is the GCD of 6 and 9 because it's the largest number they can be divided by. 

   

• 

  So we'll divide the numerator by 3. 6 divided by 3 is 2.

• 

  Then we'll divide the denominator by 3. 9 divided by 3 is 3.

• 

  Now we've reduced 6/9 to 2/3, which is its simplest form. We could also say that 6/9 is equal to 2/3.

• 

Irreducible fractions

Not all fractions can be reduced. Some are already as simple as they can be. For example, you can't reduce 1/2 because there's no number other than 1 that both 1 and 2 can be divided by. (For that reason, you can't reduce any fraction that has a numerator of 1.)

Some fractions that have larger numbers can't be reduced either. For instance, 17/36 can't be reduced because there's no number that both 17 and 36 can be divided by. If you can't find any common multiples for the numbers in a fraction, chances are it's irreducible.

Now you try it! Reduce each fraction to its simplest form.