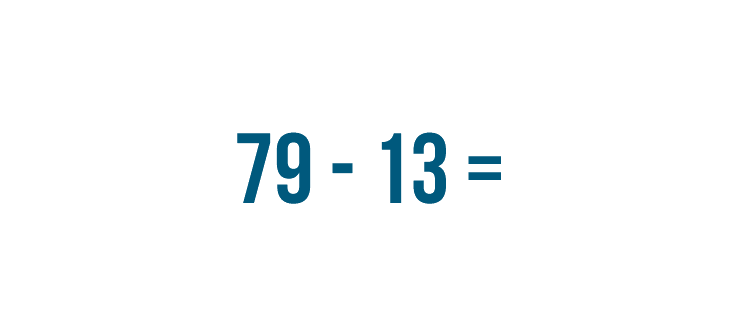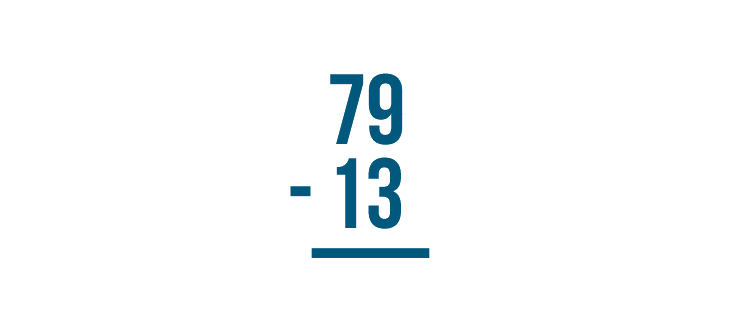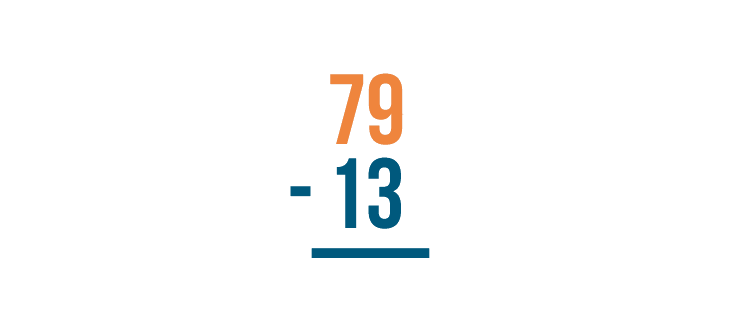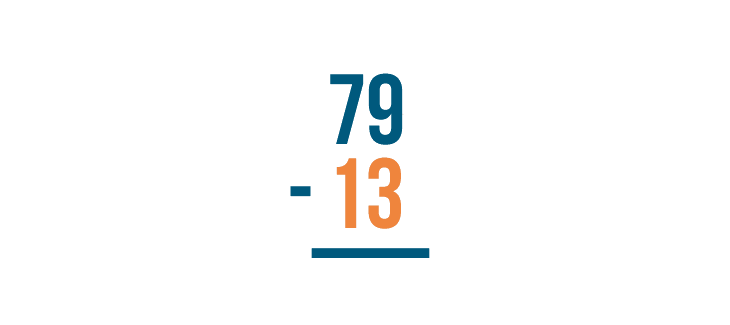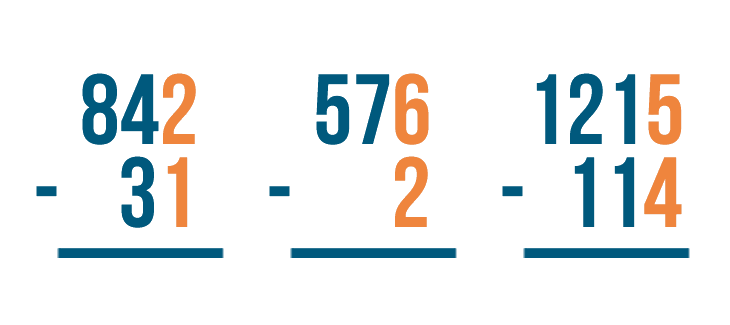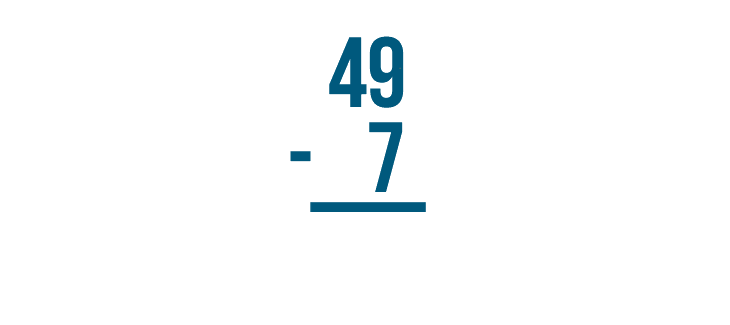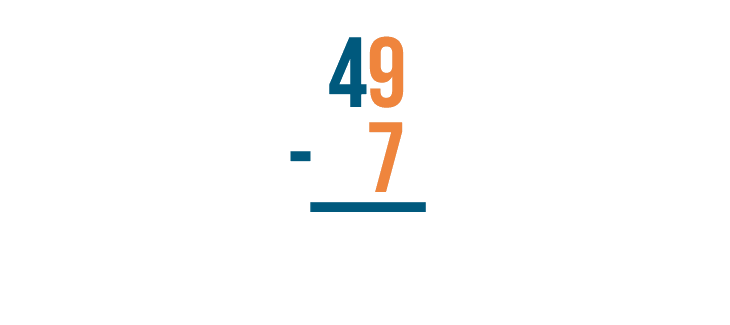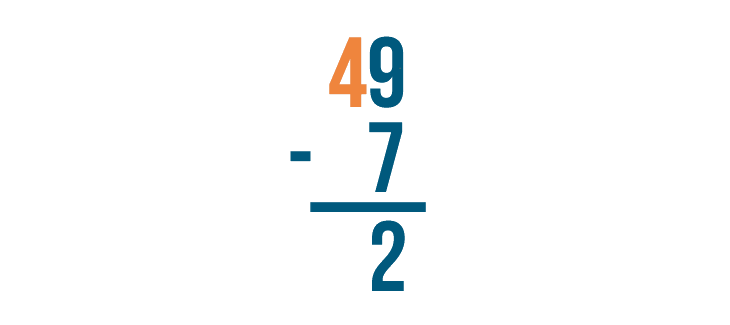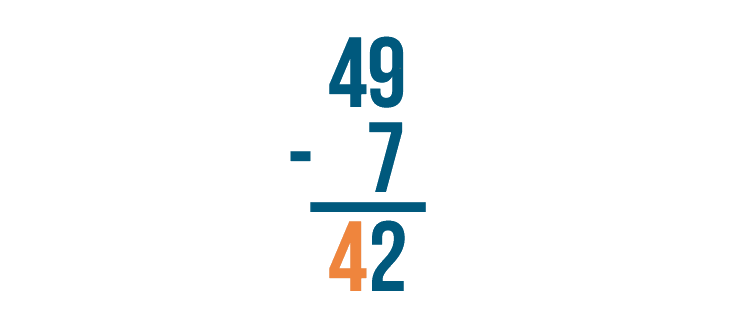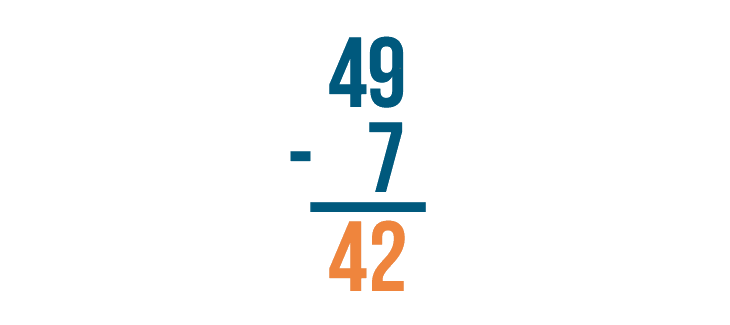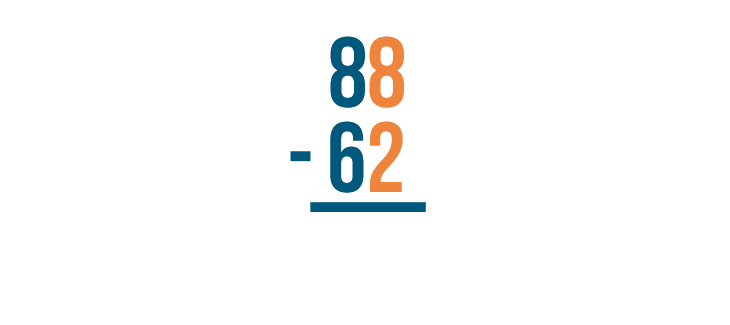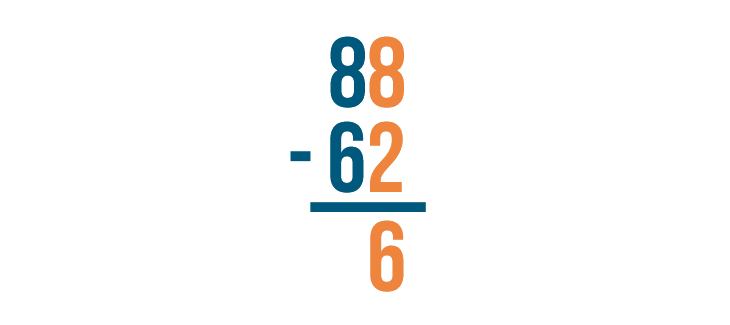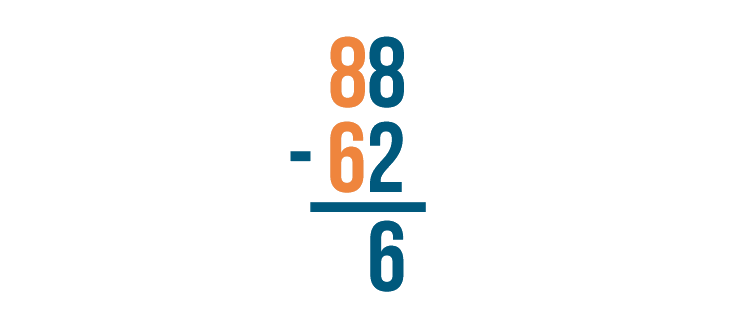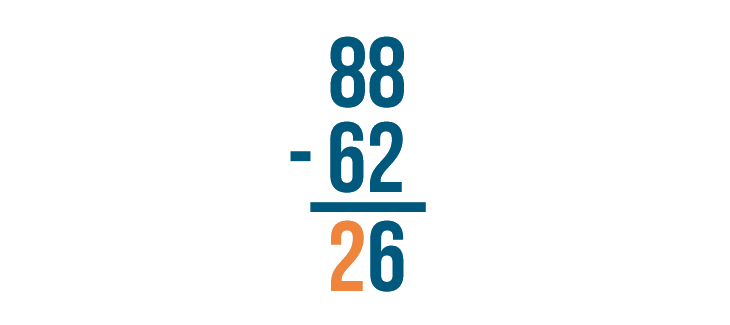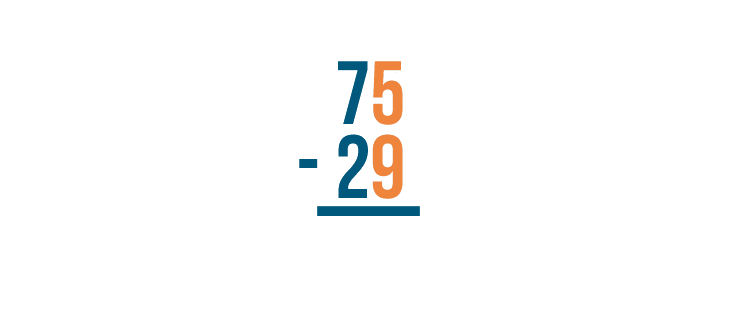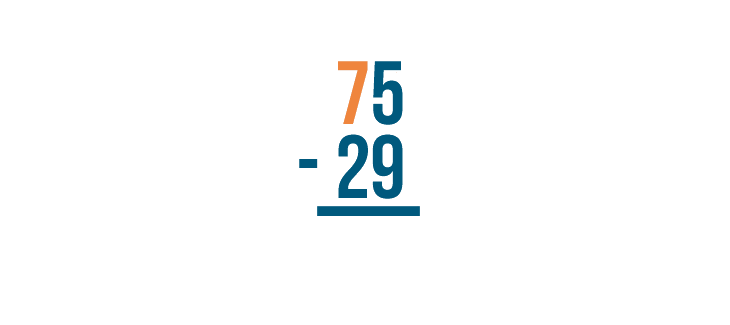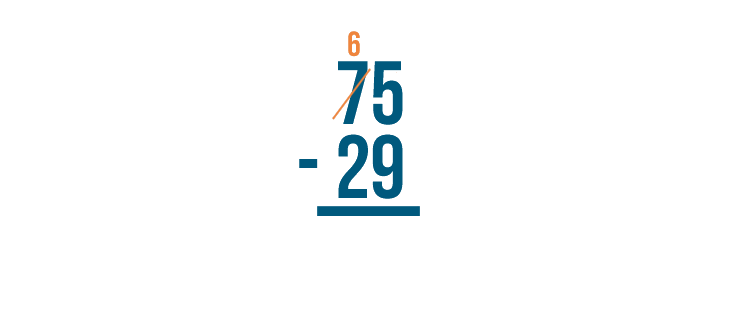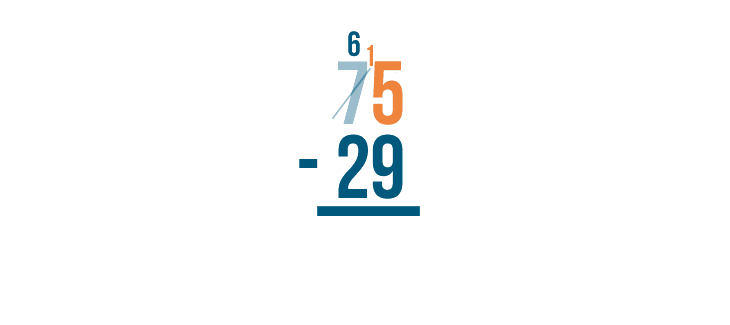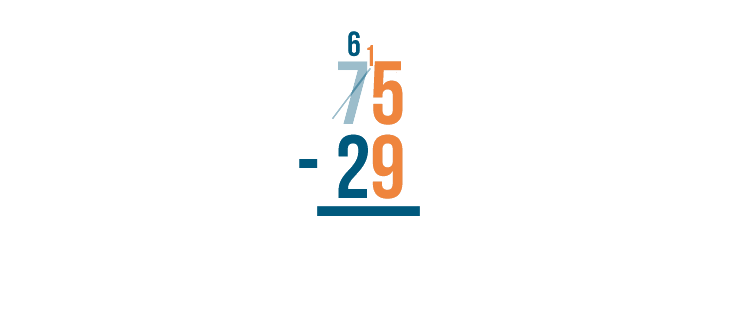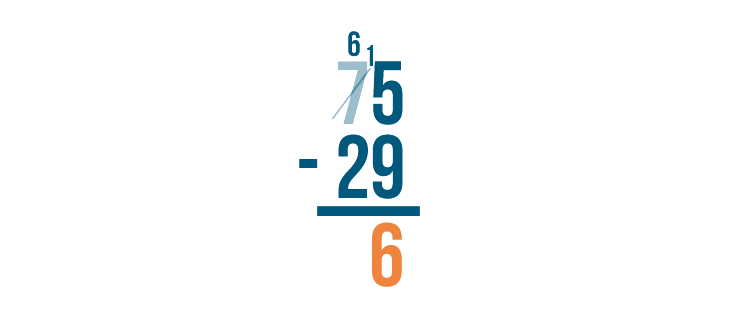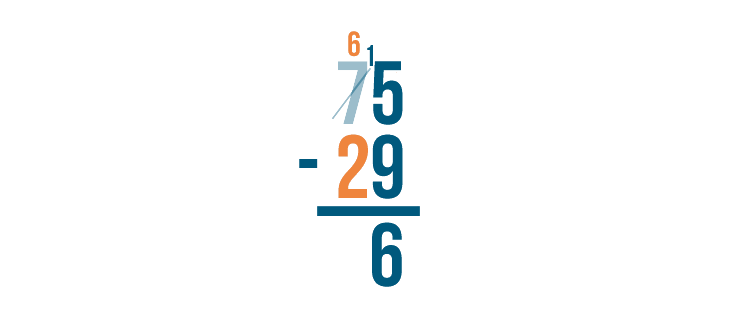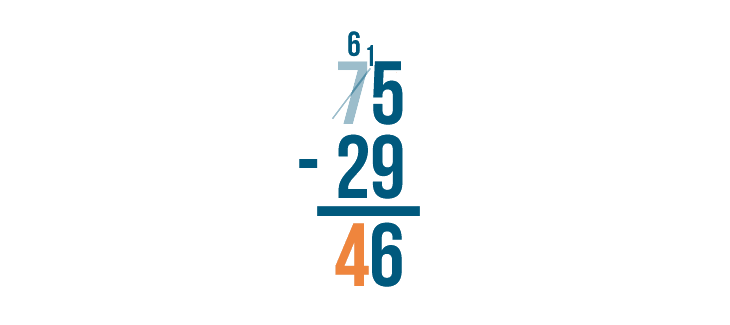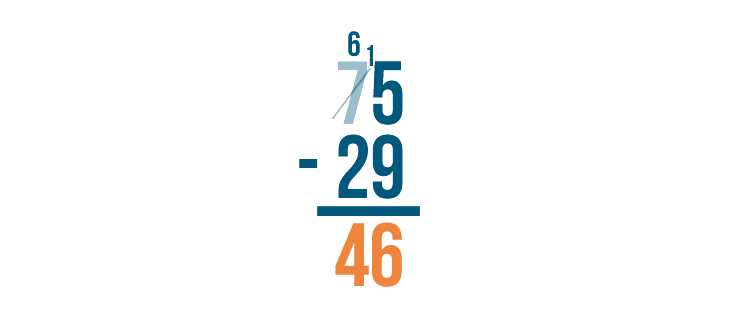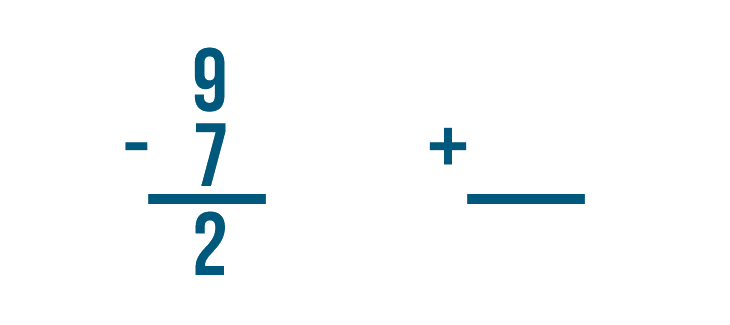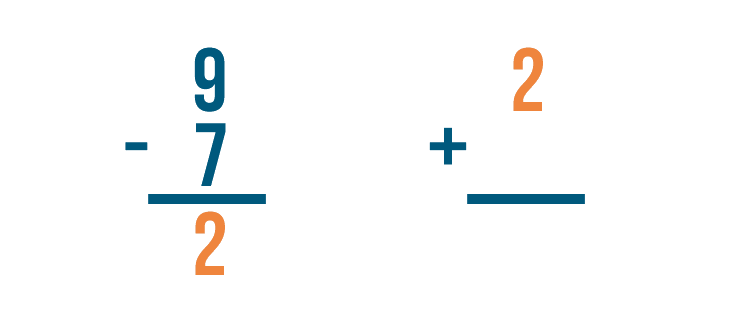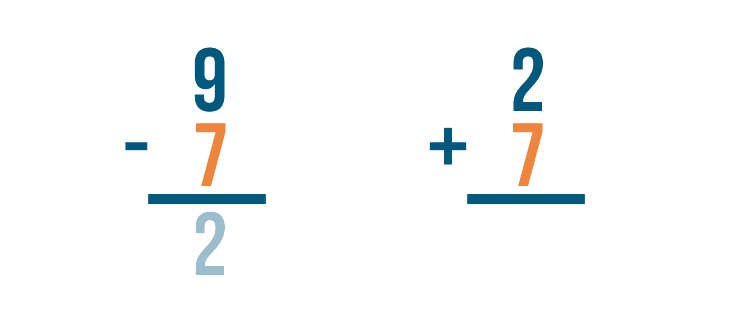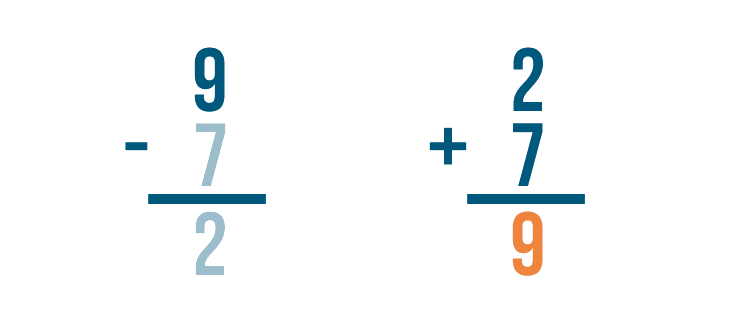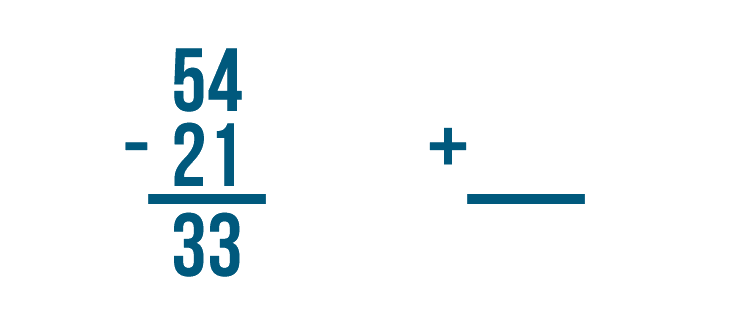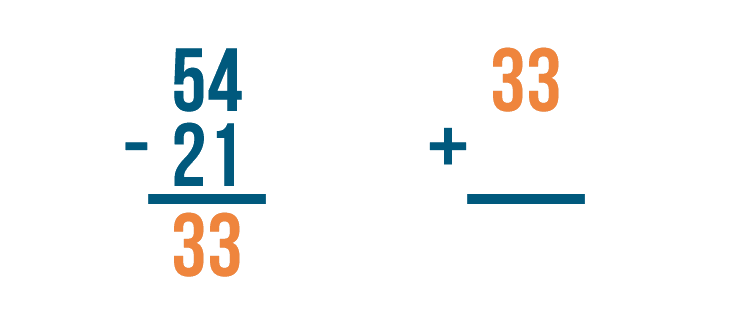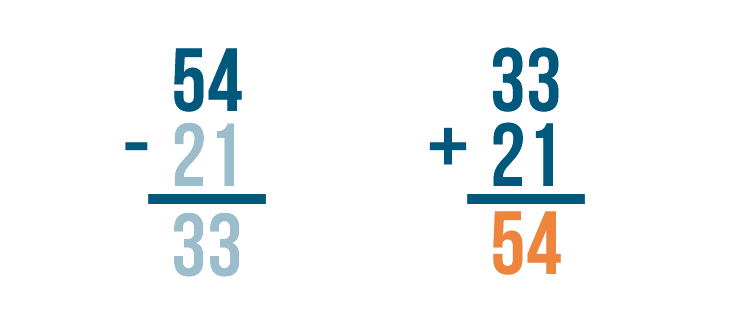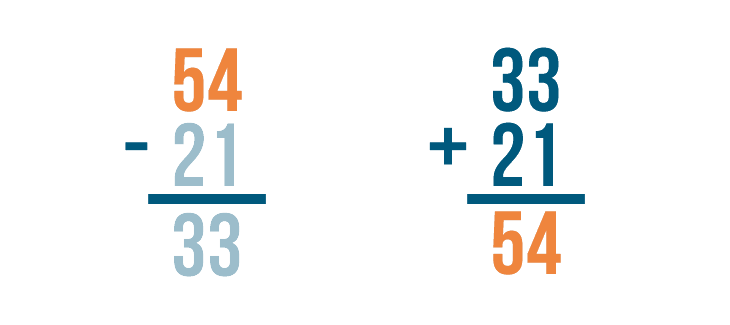Addition and Subtraction: Subtracting Two- and Three-Digit Numbers

Page 1

Subtracting Larger Numbers

In Lesson 3, we learned that counting and using visuals can be useful for solving basic subtraction problems. For instance, say you have 9 apples and you use 6 to make a pie. To find out how many apples are left, you could represent the situation like this:

It's easy to count and see that 3 apples are left.

What if you need to solve a subtraction problem that starts with a large number? For instance, let's say instead of making an apple pie, you want to pick apples from an apple tree. The tree has 30 apples and you pick 21. We could write this as 30 - 21.

You might see why counting to solve this problem isn't a good idea. When you have a subtraction problem that starts with a large number, it could take a long time to set up the problem. Imagine the time it would take to count out 30 objects and then take away 21! Also, it would be easy to lose track as you counted. You could end up with the wrong answer.

For this reason, when people solve a subtraction problem with large numbers, they set up the problem in a way that makes it easy to solve one step at a time. Let's see how this works with another problem: 79 - 13.

In the last lesson, we learned how to write expressions. However, subtracting with larger numbers is easier when the expressions are written in a different way.
Instead of writing the numbers side by side…
Place the numbers so they are stacked — one number on top and one number on the bottom.
With a stacked subtraction expression, the larger number is always written on top. Here, that number is 79.
Write the amount being subtracted underneath the top number. That's 13.
Put the minus sign to the left of the numbers.
Instead of an equals sign, put a line underneath the bottom number.
When you stack a subtraction expression, make sure the numbers are lined up correctly. They are always lined up on the right. Here, we lined up 9 and 3.
Here's another problem, 576 - 2. With this problem, see how we lined up the numbers to the right?
No matter how many digits are in the numbers, always line up the numbers to the right.

We can see that 79 - 13 and mean the same thing — they're just written differently.

Now you try stacking! Write these situations as stacked subtraction expressions. Don't solve them yet — simply set them up.

You have 272 books and you donate 60 to a library.

57 passengers are riding a bus. 24 get off at the first stop.

A clothing store has 19 scarves and sells 10.

Page 2

Solving Stacked Subtraction Problems

If you feel comfortable with the subtraction skills from Lesson 3, you're ready to start solving stacked subtraction problems.

Let's try to solve 49 - 7.
With all stacked subtraction problems, we start with the digits that are farthest to the right. Here, we'll begin with 9 and 7.
9 - 7 = 2. The difference is 2. It's important to write 2 directly beneath the digits we just subtracted.
Now let's find the difference of the digits to the left. The top digit is 4, but there's nothing beneath it.
4 minus nothing is 4, so we'll write 4 beneath the line.
Our result is 42. 49 - 7 = 42.
Let's see how this works with another problem: 88 - 62.
As always, start with the digits that are farthest to the right. Here, they are 8 and 2.
8 - 2 = 6. Make sure to write 6 below the line.
Next, find the difference of the digits to the left, 8 and 6.
8 - 6 is 2. Write 2 below the line.
The answer is 26. 88 - 62 = 26.

In the slideshow, you saw that stacked subtraction problems are always solved from right to left. The expressions below are solved the same way. First, the bottom right digit is subtracted from the top right digit. Then, the bottom left digit is subtracted from the top left digit.

85 - 24

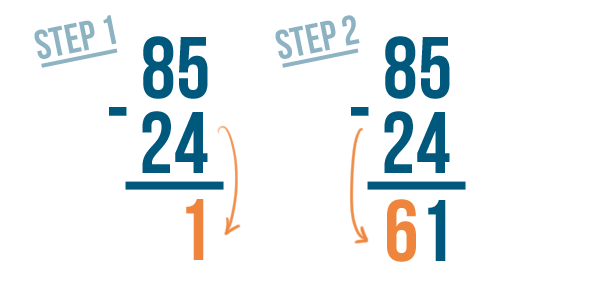
Now you try it. Solve these stacked subtraction problems.

Subtracting Larger Numbers

Stacked subtraction can also be used for finding the difference of larger numbers. No matter how many digits there are, you subtract the same way every time — from right to left.

Try it. These subtraction problems have larger numbers. Practice solving them from right to left.

Page 3

Borrowing

Can you solve this problem?

5 - 9

Of course not — 5 is smaller than 9. If you have five, it's impossible to subtract nine. In other words, you can't subtract a larger number from a smaller number.

How could you solve this next problem, then?

There's that 5 again, and 9 is beneath it. But we know that 75 is larger than 29, so we have to be able to subtract it somehow. The trick is a technique called borrowing.

Let's see how it works.

First, we'll make sure the expression is set up correctly. The larger number is stacked on top of the smaller number.
As with all stacked subtraction problems, begin with the digits farthest to the right. Here, they are 5 and 9.
5 is smaller than 9, so we'll need to borrow to make 5 larger.
We'll borrow from the digit to the left of 5. Here, it's 7. We'll take 1 from it....
7 - 1 = 6. To help us remember that we subtracted 1, we'll cross out the 7 and write 6 above it.
Then, we'll place the 1 we took next to the 5...
5 becomes 15. See how it looks like 15?
15 is larger than 9, which means we can subtract. We'll solve for 15 - 9.
15 - 9 = 6. We'll write 6 beneath the line.
Next, find the difference of the digits to the left: 6 - 2.
6 - 2 = 4. We'll write 4 beneath the line.
Our answer is 46. 75 - 29 = 46.

As you borrow, always cross out the digit you borrow from and write the new value above it. Remember to always place the 1 next to the smaller digit.

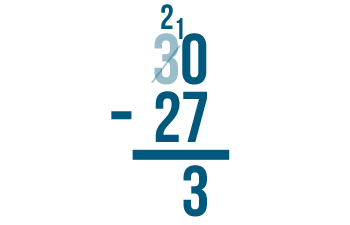
Try these problems to practice borrowing. Click the B button to borrow.

Sometimes the top number might have two or more digits that are smaller than the digits beneath them. In that case, you'll need to borrow more than once. It will always work the same way. You'll always subtract 1 from the digit to the left and place 1 next to the smaller digit.

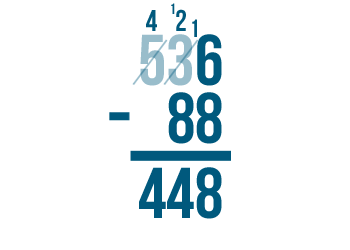
Try solving these subtraction problems to practice borrowing more than one time.

Page 4

Checking Your Work

In the last few lessons, you learned how to solve addition and subtraction problems. As you practice these math skills, it's a good idea to get into the habit of checking your work. Checking will help you know if your answers are correct. When you're ready to check the answer to subtraction problems, you'll need to use addition.

Let's look at this problem: 9 - 7 = 2.
How do we know that 2 is the correct answer? We can check by adding.
Let's set up our addition problem. First, we'll write the subtraction problem's answer. That means we'll write 2.
Next, we'll add the amount that was subtracted, 7.
Time to add. 2 + 7 = 9.
If we subtracted correctly, the answer will match the larger number in our subtraction problem.
They match — 9 and 9. Our answer was correct.
Let's try using addition to check the answer to another subtraction problem: 54 - 21 = 33.
Let's set up our addition problem. First write the answer to the subtraction problem, 33.
Then add back the number that was subtracted, 21.
Now it's time to add. 33 + 21 = 54.
Finally, we'll check to see if 54 matches the larger number in our subtraction problem. It does!