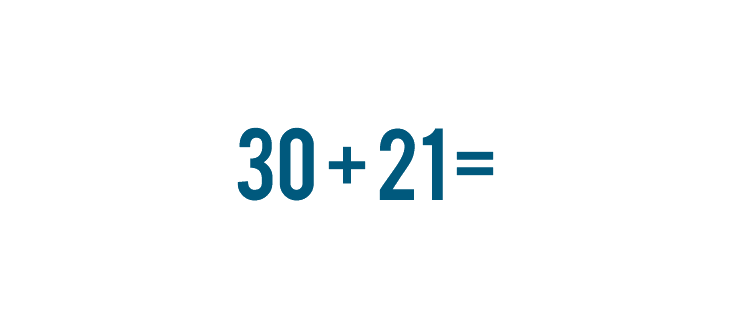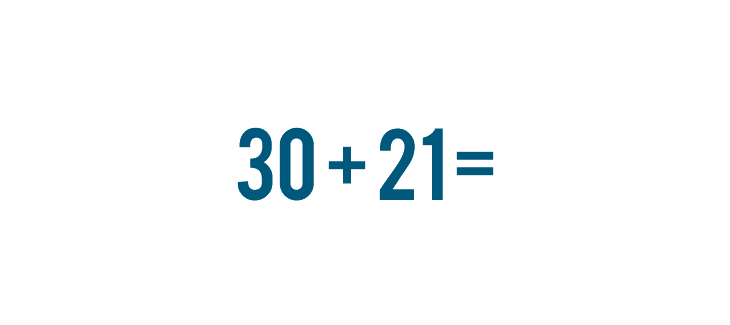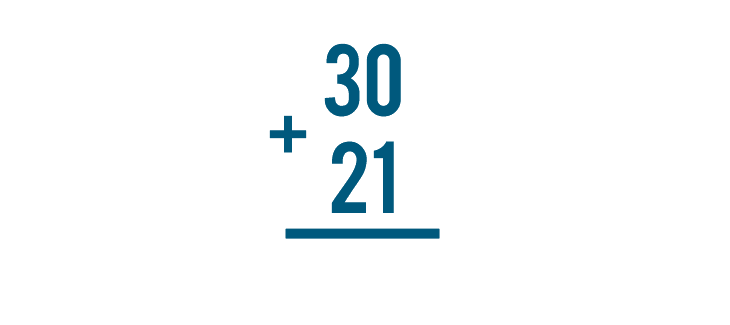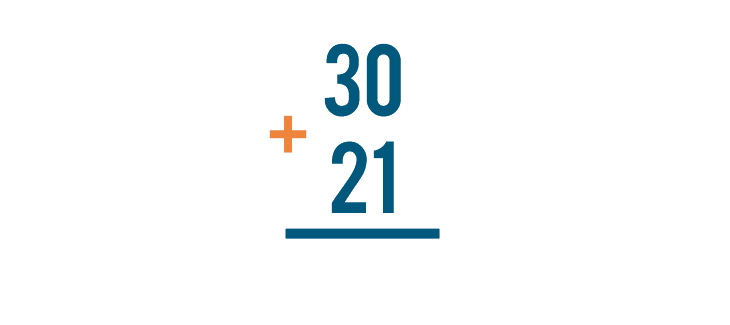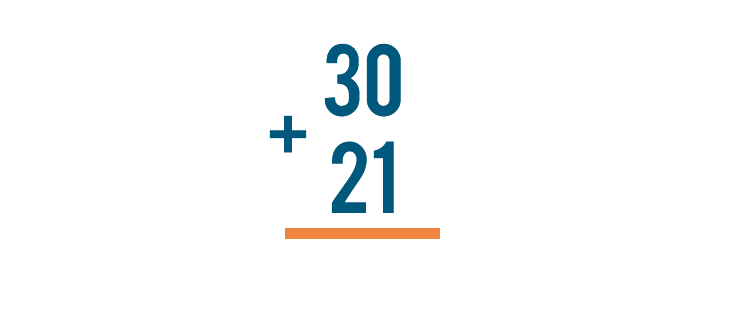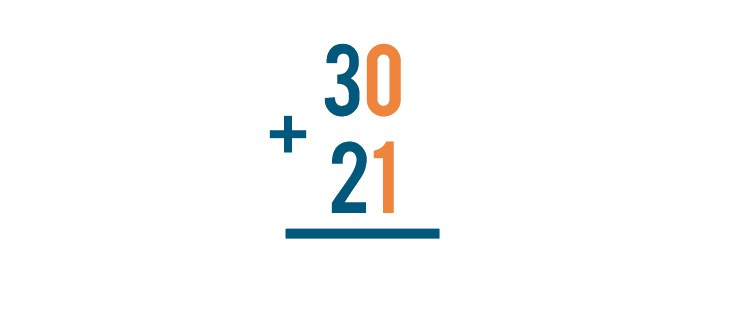Addition and Subtraction
Adding Two- and Three-Digit Numbers
Adding Larger Numbers
As we saw in Lesson 1, you can often use counting and visuals to solve basic addition problems. For instance, imagine that 3 people are going on a trip and 2 more decided to join. To find out how many people were going total, you could represent the situation like this:
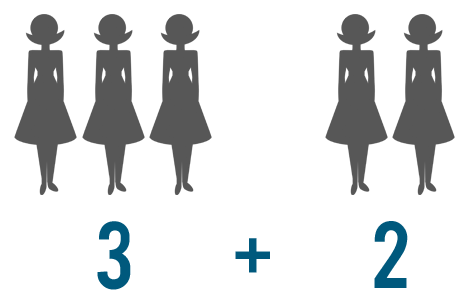
Once you look at the problem visually, you can count and see that 5 people are going on the trip.
What if you have a bigger problem to solve? Imagine that a few groups of people are going somewhere together. 30 people travel on one bus, and 21 travel on another. We could write this as 30 + 21.

It might not be a good idea to solve this problem by counting. First of all, no matter how you choose to count, it would probably take a pretty long time to set up the problem. Imagine drawing 30 and 21 pencil marks on the page, or counting out that many little objects! Second, actually counting the objects could take long enough that you might even lose track.
For this reason, when people solve a large addition problem, they set up the problem in a way that makes it easier to solve one step at a time. Let's look at the problem we discussed above, 30 + 21.
We can see that 30 + 21 and 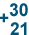 mean the same thing. They're just written differently.
mean the same thing. They're just written differently.
Now you try it. Write these situations as vertically stacked expressions. Don't solve them yet — just set them up.
On the first day of school, a teacher has 21 students in her class. On the second day, two more students join the class.
A clothing store sells 32 pairs of red pants and 51 pairs of blue pants.
112 people bought tickets to a play in advance. 62 bought tickets on the day of the play.